Our Blogs
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.
How to choose the best BPO Company
There are many variations of passages about dummy about Lorem Ipsum.
02How You Can Get Loan Easily For Your Business
There are many variations of passages about dummy about Lorem Ipsum.
03I Have Explain A Digital Customer Experience
There are many variations of passages about dummy aboutLorem Ipsum available.
04You Can Present Your Business Growth
There are many variations of passages about dummy aboutLorem Ipsum available.
05Cloud Growing Your Business
There are many variations of passages about dummy about Lorem Ipsum available.
06How You Can Get Loan Easily For Your Business
There are many variations of passages about dummy aboutLorem Ipsum available but the majority suffered randomiseds.
07How To Become Top Conference For Business
There are many variations of passages about dummy aboutLorem Ipsum available but the majority suffered randomiseds.
08How to choose the best BPO Company
There are many variations of passages about dummy about Lorem Ipsum.
09Why Is Outbound Call Center Outsourcing
Dummy about Lorem Ipsum There are many variations of passages about .
10Get New Features For Better Experience
The majority suffered rando miseds dummy about Lorem Ipsum available .
11Hello world!
Welcome to WordPress. This is your first post. Edit or delete it, then start writing!
12Hello world!
Welcome to WordPress. This is your first post. Edit or delete it, then start writing!
13Mixed Quantitative Aptitude Questions Set 246
[WpProQuiz 330]
Previous Post:→ The Hindu Editorial Vocabulary – Set 190
Previous Quant Post:→ Mixed Quantitative Aptitude Questions Set 245
14Mixed Quantitative Aptitude Questions Set 245
- A and B can do a work in 12 days. B and C can do the same work in 20 days. A and C can also do the same work in 30 days. If they all work together in how many days will they complete the work ?
12 days8 days14 days18 days17 daysOption A
LCM of 12, 20 and 30 = 120
efficiency of A and B = 120/12 = 10
efficiency of B and C = 120/20 = 6
efficiency of A and C = 120/30 = 4
2(A + B + C) = 20
A + B + C = 10
time = 120/10 = 12 days - Sujit, Rajat and Sanjay started a partnership business rs.8400 , rs.5000 and rs.6000 respectively. If they invested their capital for 5 months, 6 months and 8 months respectively and total profit of the business is rs. 2000, then how much profit Sanjay got at the end of the year ?
400580420800750Option D
Profit sharing ratio of Sujit, Rajat and Sanjay = (8400 * 5) : (5000 * 6) : (6000 * 8) = 7 : 5 : 8
profit of Sanjay = 2000/20 * 8 = 800 - Total income of A, B and C is rs.9400. If A’s income is 4/5th of B’s income and B’s income is 3/4th of C’s income, then find the income of A.
18002200280024003500Option D
A/B = 4/5
B/C = 3/4
by balancing, A/B = 4 *3/5 *3 = 12/15
B/C = 3 *5/4*5 = 15/20
ratio of A, B and C = 12 : 15 : 20
A’s income = 9400 * 12/47 = 2400 - Pipes And B together can fill a tank in 20 hours while pipe A alone can fill the same tank in 30 hours. Find how much time taken by B to fill the same tank ?
40 hours30 hours60 hours45 hours50 hoursOption C
LCM of 20 and 30 = 60
let capacity of tank = 60
efficiency of pipe A and B together = 60/20 = 3
efficiency of pipe A = 60/30 = 2
efficiency of pipe B = 3 – 2 = 1
time taken by B to fill the tank = 60/1 = 60 hours - Boat A covers 180 km in downstream in 9 hours. If the speed of boat in still water is 12 km/hr, then find time taken by boat A to cover 96 km in upstream ?
12 hours13 hours22 hours24 hours15 hoursOption D
Downstream speed = 180/9 = 20 km/hr
speed of boat = 12 km/hr
speed of stream = 20 – 12 = 8 km/hr
upstream speed = 12 – 8 = 4 km/hr
time = 96/4 = 24 hours - I. x^2 – 11x – 80 = 0
II. y^2 – 20y + 64 = 0X > YX < YX ≥ YX ≤ YX = Y or no relations.Option E
I. x^2 – 16x + 5x – 80 = 0
x = 16 , -5
II. y^2 – 16y – 4y + 64 = 0
y = 16, 4 - I. x^2 = 196
II. y^2 – 19y + 70 = 0X > YX < YX ≥ YX ≤ YX = Y or no relations.Option E
I. x^2 = 196
x = 14, -14
II. y^2 – 14y – 5y + 70 = 0
y = 14, 5 - I. 3x^2 – 13x + 12 = 0
II. 2y^2 + 14y +12 = 0X > YX < YX ≥ YX ≤ YX = Y or no relations.Option A
I. 3x^2 – 9x – 4x + 12 = 0
3x = 9, 4
x = 3, 1.33
II. 2y^2 + 14y + 12 = 0
2y = -12, -2
y = -6, -1 - I. 2y^2 – 11y + 15 = 0
II. x^2 + 5x + 4 = 0X > YX < YX ≥ YX ≤ YX = Y or no relations.Option B
I. 2y^2 – 6y – 5y + 15 = 0
2y = 6, 5
y = 3, 2.5
II. x^2 + 4x + x + 4 = 0
x = – 4, -1 - I. x^2 – 28 = 36
II. y^3 = 512X > YX < YX ≥ YX ≤ YX = Y or no relations.Option D
I. x^2 = 64
x = 8, -8
II. y^3 = 512
y = 8
Previous Post:→ Static GK Quiz for Upcoming Exams Set – 627
Previous Quant Post:→ Mixed Quantitative Aptitude Questions Set 244
15Mixed Quantitative Aptitude Questions Set 244
- A vessel has only two types of oil A and B in the ratio of 9 : 7 respectively. When 25 liters of oil is added to the vessel then quantity of oil A becomes 75% of that of oil B. What is the capacity of vessel if it becomes full after addition of 25 liters oil ?
120 lt105 lt100 lt130 lt80 ltOption B
Let quantity of oil in vessel A and B = 9x and 7x
9x = (7x + 25) 75/100
36x = 21x + 75
15x = 75
x = 5
capacity of vessel = 9x + 7x + 25 = 105 liters - The ratio of present age of A and B is 6 : 5 and the present age of C is 5 years less than B. After 6 years the age of A is two times the present age of C. If the present age D is 8 years more than B, then find the present age of D ?
26 years30 years28 years23 years32 yearsOption C
Let the present age of A and B = 6x and 5x respectively.
present age of C = 5x – 5
ATQ, 6x + 6 = (5x – 5) * 2
6x + 6 = 10x – 10
x = 4
present age of D = 5x + 8 = 28 years - P and Q together can complete a work in 24 days and Q and R together can complete the same work in 30 days. P and R together work for 15 days and after 15 days P and R left the work remaining work done by done B. If the efficiency ratio of P and Q is 2 : 3, then find in how many days total work will be completed ?
28 days60 days40 days38 days25 daysOption C
LCM of 24 and 30 = 120
total work = 120
efficiency of P and Q = 120/24 = 5
efficiency of Q and R = 120/30 = 4
efficiency of P = 5 * 2/5 = 2
efficiency of Q = 5 – 2 = 3
efficiency of R = 4 – 3 = 1
P and R together work for 15 days = ( 2 + 3) * 15 = 45 work
remaining work = 120 – 45 = 75
days required by B to complete remaining work = 75/3 = 25 days
total days = 15 + 25 = 40 days - A and B entered into a partnership business by investing rs.12000 and rs.14000 respectively. After x months C joined then by investing rs. 8000 and B left the business. If profit earned by C at the end of year is rs. 800 out of total profit rs.7200, then find for how many months did C invest his money ?
8 months4 months2 months7 months6 monthsOption B
Profit sharing ratio = (12000 * 12) : (14000 * x) : (8000 * 12 – x)
= 144 : 14x : 96 – 8x
96 – 8x/144 + 14x = 1/8
144 + 14x = 768 – 64x
78x = 624
x = 8
C invest his money for 12 – 8 = 4 months - Rohit calculates his profit percentage on SP while Sumeet calculate his profit percentage on CP. They find that the difference between their profit is rs.280. If SP of both are same and both get 20% profit, then find CP of Rohit ?
1240014000150001080012000Option D
Let SP of both Rohit and Sumeet = rs.100x
profit of Rohit = 100x * 20/100 = 20x
CP of Rohit = 80x
CP of Sumeet = 100x/120 * 100 = 500x/6
Rohit of Sumeet = 100x – 500/6 = 50x/3
20x – 50x/3 = 450
x = 135
CP of Rohit = 135 * 80 = 10800 - Directions : What will come in place of questions (?) marks in the following questions given below ? (you are not calculate exact value)
49.96% of 1740 + 28% of 1200 – √1764.05 + 120 = ?13401250133612841265Option D
870 + 336 – 42 + 120 = ?
? = 1284 - 4799.98 – 320% 400 – √1331 + 3700/50 = ?
36423485239452503583Option E
4800 – 1280 – 11 + 74 = ?
? = 3583 - (35 * 24) + (40 * 28) – (38)^2 + ? = 800
384360538284264Option D
840 + 1120 – 1444 + ? = 800
516 + ? = 800
? = 284 - 520% of 180 – ( 42 * 25) + 376 = ?
275263340345262Option E
936 – 1050 + 376 = ?
? = 262 - 387.04 + 19.99% of 230 – 1540/19.95 + ? = 420
5664628448Option B
387 + 46 – 77 + ? = 420
? = 64
16
Mixed Quantitative Aptitude Questions Set 243
- 8 men and 6 women together can complete a piece of work in 20 days. If the efficiency of a man is 50% more than efficiency of a woman, then find in how many days 12 men and 14 women can complete the same piece of work ?
14 days12.5 days90/7 days90/8 days18 daysOption D
Efficiency ratio of a man and a woman = 3 : 2
total work =( 8 * 3 + 6 * 2) * 20 = 720 work
days required to complete work by 12 men and 14 women = 720/(12 * 3 + 14 * 2) = 90/8 days - A bag contains 72 balls out of which green balls are 28 and orange balls are x and remaining balls are pink. If two balls are randomly picked up from the bag then the probability of getting green ball and a orange ball is 56/213. Find the number of pink balls in that bag ?
1422182520Option E
No. of green balls = 28
no.of orange balls = x
no.of pink balls = 72 – (28 + x) = 44 – x
probability = (28C1) * (xC1)/72C2 = 56/213
28 * x * 2/72 * 71 = 56/213
x = 24
no. of pink balls = 44 – 24 = 20 - Ranju goes from home to office at speed of (x + 25) km/h and returns with a speed of (x + 10) km/h. If average speed of Ranju for the whole journey is 36 km/h, then find time taken by him to cover a distance of 140 km if his speed is (x + 8) km/h ?
4 hours5 hours8 hours2 hours6 hoursOption B
2 (x + 25) (x + 10)/x + 25 + x + 10 = 36
x^2 + 10x + 25x + 250 = 36x + 630
x^2 – x – 380 = 0
x = 20, -19
x = 20
time = 140/20 + 8 = 5 hours - A and B started a business by investing certain sum in the ratio of 7 : 6 for 5 months and 6 months respectively. If total profit of the business is rs.2840, then find how much amount investment by A in the business ?
35003200430044002800Option E
Let investment amount at A and B is 7x and 6x respectively.
profit sharing ratio of A and B = (7x * 5 : 6x * 6) = 35x : 36x
71x = 2840
x = 40
amount invested by A = 40 * 7 = 2800 - A person purchased rice at rs. 8 rs. 12 and rs.20 per kg in three consecutive years. If he spent rs.2400 each year on rice, then find the approximate average cost per kg paid by him in the given three consecutive years.
121111 19/3112 19/3514Option C
Quantity of rice purchased by him in 1st year = 2400/8 = 300kg
2nd year = 2400/12 = 200 kg
3rd year = 2400/20 = 120 kg
total quantity purchased = 300 + 200 + 120 = 620
total amount paid = 2400 * 3 = 7200
average = 7200/620 = 11 19/31 - Directions : In each of these questions, two equation (I) and (II) are given. You have both the equations and give answer.
I. x^2 – x – 380 = 0
II. y^2 + 29y + 210 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option E
I. x^2 – 20x + 19x – 380 = 0
x = 20, -19
II. y^2 + 15y + 14y + 210 = 0
y = -15, -14 - I. y^2 – 18y + 72 = 0
II. x^2 – 31x + 238 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option A
I. y^2 – 12y – 6y + 72 = 0
y = 12, 6
II. x^2 – 17x – 14x + 238 = 0
x = 17 , 14 - I. x^2 – 8√2 + 30 = 0
II. y^2 – 7√2 + 24 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option E
I. x^2 – 5√2 – 3√2 + 30 = 0
x = 5√2, 3√2
II. y^2 – 4√2- 3√2 + 24 = 0
y = 4√2, 3√2 - I. x^2 = 1024
II. y = √1764X > YX < YX ≥ YX ≤ YX = Y or no relation.Option B
I. x^2 = 1024
x = 32, -32
II. y = √1764
y = 42 - I. y^3 = 2197
II. x^2 + 50 = 275
X > YX < YX ≥ YX ≤ YX = Y or no relation.Option E
I. y^3 = 2197 X > Y
y = 13
II. x^2 = 275 – 50 = 225
x = 15, -15
Previous Post:→ The Hindu Editorial Vocabulary – Set 166
Previous Quant Post: → Mixed Quantitative Aptitude Questions Set 242
17Mixed Quantitative Aptitude Questions Set 242
- The discount allowed on an article is rs.960 more than the profit earned on the article. If the selling price of the article is rs.1920 and shopkeeper marked the article 100% above its cost price, then find profit% earned on the article.
10%20%12%18%40%Option B
Let cost price of the article = rs.100x
MP = 100x *2/1 = 200x
ATQ, (200x – 1920 ) – (1920 – 100x) = 960
300x = 4800
x = 16
CP = 1600
Profit % = 1920 – 1600/1600 * 100 = 20% - The height of cylinder is equal to the side of square. If area of square is 196m^2 and ratio and ratio of radius to height of cylinder is 3 : 2, then find total surface area of such cylinder.
56306450342046206430Option D
Side of square = √196 = 14m
height = 14m
radius = 14/7 * 6 = 21
TSA = 2πr ( h + r)
= 2 * 22/7 * 21(14 + 21)
= 4620 - A man invested rs. P and (P + 350) each at the rate of 20% p.a on CI and SI respectively for two years. If ratio of total CI to total SI received by man is 44 : 75, then find amount invested by man on CI ?
1050840450400800Option D
Rate of CI for 2 years = 20 + 20 + 20 *20/100 = 44%
CI received = P * 44/100 = 44P/100
SI received by man = ( P + 350) 40/100 = 40P + 14000/100
44P/40P + 14000 = 44/75
P = 400 - If three unbiased coins are tossed simultaneously, then find the probability of getting at most two heads ?
3/57/82/54/72/17Option B
Total outcome = 2^3 = 8
favorable outcome = 7
probability = 7/8 - Pipe A and B alone can fill a tank in 20 hours and 24 hours respectively and outlet pipe C can empty same tank in 40 hours. If three pipes are opened simultaneously in how much time required to fill a empty tank ?
20 hours15 hours18 hours14 hours28 hoursOption B
LCM of 20, 24 and 40 = 120
efficiency of A = 120/20 = 6
efficiency of B = 120/24 = 5
efficiency of C = 120/40 = 3
time required = 120/(6 + 5) – 3 = 15 hours - Directions : What will come in place of questions marks (?) in the following number series ?
85, 104, 189, 293, 482, ?875775456565235Option B
The series is, (85 + 104), (104 + 289), (189 + 293), (293 + 482) - 8, ?, 6, 15, 52.5, 236.25
544.52.56Option B
The series is, (* .5), (* 1.5), (* 2.5), (* 3.5), (* 4.5) - ?, 2, 3, 8, 35, 204
24568Option A
The series is, (* 2 – 2), (* 3 – 3), (* 4 – 4), (* 5 – 5), (* 6 – 6), - 27, ?, 159, 324, 555, 852
6086783480Option A
The series is, difference of difference. - 68, 92, 66, 94, 64, ?
84901029686Option D
The series is, (+ 24), (- 26), (+ 28), (- 30), (+ 32)
Previous Post:→ Daily Current Affairs 7th December, 2021
Previous Quant Post:→ Mixed Quantitative Aptitude Questions Set 241
18Mixed Quantitative Aptitude Questions Set 241
- A bag contains (x + 1), green balls and (x + 4) yellow balls. If one ball is drawn at random from the bag, the probability of getting a green ball is 3/7. Find the total number of balls in the bag ?
3423284221Option E
Probability = 3/7
x + 1/x + 1 + x + 4 = 3/7
x + 1/2x + 5 = 3/7
x = 8
total balls in the bag = 9 + 12 = 21 balls - A alone can do a work in 20 days and efficiency of A is 7 1/7% more than B. If efficiency of C is 20% less than A, then find in how many days B and C together can complete the same work ?
100/9 days15 days18 days200/3 days30 daysOption A
Fraction value 7 1/7% = 1/14
efficiency of B = 14
efficiency of A = 15
total work = 15 * 20 = 300
efficiency of C = 15 * 4/5 = 12
time = 300/15 + 12 = 100/9 days - The ratio of milk and water in a mixture is 11 : 4. When 30 liters of mixture is taken out and 18 liters of milk is added in the remaining mixture, the ratio of milk to water is 5 : 1, find the initial quantity of milk.
44 liters65 liters40 liters50 liters62 litersOption A
Let quantity of milk = 11x
and water = 4x
(11x – 30 * 11/15 + 18)/4x – 30 * 4/15 = 5/1
11x – 4/4x – 8 = 5/1
11x – 4 = 20x – 40
x = 4
initial quantity of milk = 11 * 4 = 44 liters - An amount is divided among A, B and C, amount of B is average of amount A and C and when amount of B is reduced by 20% of that of A, it becomes equal to that of C. Find amount of C is what percent of total amount ?
20%30%40%15%25%Option E
Let amount of A and C is rs.x and rs.y respectively.
amount of B = x + y/2
x + y/2 – x/5 = y
3x = 5y
x/y = 5/3
amount of A = rs.5a
amount of B = rs.4a
amount of C = rs.3a
% = 3a/12a * 100 = 25% - Train A running at speed of 108 km/hr crosses a platform having twice the length of train in 24 sec. Train B whose length is 420m crosses same platform in 36 sec, then find the speed of train B ?
108 km/hr45 k/hr76 km/hr90 km/hr72 km/hrOption D
Let length of train A = x
length of platform = 2x
x + 2x/24 = 108 * 5/18
x = 240m
let speed of train B is y km/hr
420 + 2 * 240/36 = y * 5/18
y = 90 km/hr - Directions : In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give answer
I. x^2 – 17x – 84 = 0
II. y^2 + 4y – 117 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option E
I. x^2 – 21x + 4x – 84 = 0
x = 21, -4
II. y^2 + 13y – 9y – 117 = 0
y = -13, 9 - I. x^2 + 23x + 132 = 0
II. y^2 + 21y + 110 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option D
I. x^2 + 12x + 11x + 132 = 0
x = -12, -11
II. y^2 + 11y + 10y + 110 = 0
y = -11, -10 - I. x^2 = 196
II. y = √196X > YX < YX ≤ YX ≥ YX = Y or no relation.Option C
I. x^2 = 196
x = 14, -14
II. y = √196
y = 14, 14 - I. 3x^2 + 13x + 12 = 0
II. y^2 + 9y + 20 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option A
I. 3x^2 + 9x 4x + 12 = 0
3x = -9, -4
x = -3, -1.33
II. y^2 + 5y + 4y + 20 = 0
y = -5, -4 - I. x^3 = 216
II. 2y^2 – 25y + 78 = 0X > YX < YX ≥ YX ≤ YX = Y or no relation.Option D
I. x^3 = 216
x = 6
II. 2y^2 – 13y – 12y + 78 = 0
2y = 13, 12
y = 6.5, 6
19
Mixed Quantitative Aptitude Questions Set 240
- Directions : What will come in place of questions mark (?) in the following questions. (You are not calculate exact value )
∛216.84 – 23 * 3 + (8.99)^3 = ?684673573275680Option B
13 – 69 + 729 = ?
? = 673 - 24.86% of 168 * 5.04 + (12.02)^2 – 19.81 = ?
284224342334128Option D
1/4 * 168 * 5 + 144 – 20 = ?
? = 334 - 14.28% of 279.86 * 15 + 21 * 4.05 = ?
285684234724580Option B
40 * 15 + 84 = ?
? = 600 + 84
? = 684 - 32% of 374.98 + 644.02 ÷ 23 + 185.99 = ?
334234134448528Option A
32% of 375 + 28 + 186 = ?
? = 120 + 28 + 186
? = 334 - (22)^2 + (28)^2 – (15)^2 = ?
1245104310508451440Option B
484 + 784 – 225 = ?
? = 1043 - Directions : In each of these questions, two equations (I) and (II) are given. You have to solve both the equations and give answer.
I. 5x^2 + 11x + 2 = 0
II. 4y^2 + 13y + 3 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. 5x^2 + 10x + x + 2 = 0
5x = – 10 , – 1
x = -2, -.2
II. 4y^2 + 12y + y + 3 = 0
4y = -12, – 1
y = -3, .25 - I. x^2 + 5x + 6 = 0
II. y^2 + 9y + 14 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. x^2 + 3x + 2x + 6 = 0
x = -3, -2
II. y^2 + 7y + 2y + 14 = 0
y = -7, -2 - I. x^2 – 11x + 30 = 0
II. y^2 – 15y + 56 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption B
I. x^2 – 6x – 5x + 30 = 0
x = 6, 5
II. y^2 – 7y – 8y + 56 = 0
y = 7, 8 - I. x^2 + 17x + 72 = 0
II. y^2 + 13y + 42 = 0
X > YX < YX ≥ YX ≤ YX = Y or no relationOption B
I. x^2 + 9x + 8x + 72 = 0
x = -9, -8
II. y^2 + 7y + 6y + 42 = 0
y = -7, -6 - I. x^2 + 23x + 132 = 0
II. y^2 + 21y + 110 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption D
I. x^2 + 12x + 11x + 132 = 0
x = -12, -11
II. y^2 + 11y + 10y + 110 = 0
y = -11, -10
20
Mixed Quantitative Aptitude Questions Set 239
- A train , 240 m long crosses a man, walking along the line in opposite direction at the rate of 3 km/hr in 10 seconds. What is the speed of train ?
80 km/hr75 km/hr83.4 km/hr92.8 km/hr68 km/hrOption C
Let speed of train = x m/hr
240/(3 + x) 5/18 = 10
x = 83.4 km/hr - A boat takes a total of 24 hours to over 90 km in downstream and 90 km in upstream. If the ratio of speed of boat in sill water and speed of stream is 4 : 1, then find how much time is required to cover 120 km distance in down stream speed ?
8 hours14 hours20 hours15 hours12 hoursOption E
Let speed of boat in still water = 4x
speed of stream = x
downstream speed = 4x + x = 5x
upstream speed = 4x – x = 3x
90/5x + 90/3x = 24
x = 2
downstream speed = 5 * 2 = 10 km/hr
time = 120/10 = 12 hours - A equilateral tringle and a square have the same area. If the perimeter of the square is 88cm, then find what is area of the equilateral tringle ?
196 cm^2256 cm^2144 cm^2484 m^2125 cm^2Option D
Perimeter of square = 88cm
side of square = 88/4 = 22cm
area of square = 22 * 22 = 484 cm^2
area of tringle = 484 cm^2 - Pipe A can fill a tank in 15 hours and pipe B can fill the same tank in 60 hours, pipe C can empty in 10 hours. Pipe A and B are kept opened for 10 hours in the beginning and then pipe C is also opened, what is the time taken to empty the tank ?
60 hours40 hours30 hours25 hours50 hoursOption E
Capacity of the tank = 15, 60, 10 = 60 units
efficiency of pipe A = 60/15 = 4 units
efficiency of pipe B = 60/60 = 1
efficiency of pipe C = 60/10 = 6 units
tank filled in 1st 10 hours = (4 + 1) * 10 = 50 units
now, when all the pipe work together, 1 unit of water will out in every minute from tank.
50 units of water will be in 50 hours. - The ratio of age of A and B, 6 years ago was 3 : 4. Sum of the present age of B and C is 80 years. C is 12 years elder to A. Find the difference of age of B and C after 4 years ?
5 years6 years8 years4 years12 yearsOption D
6 years ago age of A = 3x
age of B = 4x
present age of A = 3x + 6
present age of B = 4x + 6
present age of C = 3x + 6 + 12 = 3x + 18
4x + 6 + 3x + 18 = 80
7x = 56
x = 8
age of B after 4 years = 4x + 6 + 4 = 42 years
age of C after 4 years = 3x + 18 + 4 = 46 years
difference = 46 – 42 = 4 years - Directions : What will be wrong number in the following wrong number series ?
120, 83, 113, 93, 105, 99, 1011138310512099Option D
The series is, (- 6 * 7), (+ 5 * 6), ( – 4 * 5), ( + 3 * 4), ( – 2 * 3), ( + 1 * 2) - 1898, 1870, 1657, 1608, 1096, 1015, 15
109610151898151870Option E
The series is ( – 5^2 ), (- 6^3), (- 7^2), (- 8^3 ), (- 9^2), (- 10^3) - 48, 84, 156, 300, 590, 1164
481563005901164Option D
The series is, ( * 2 – 12), ( * 2 – 12)… - 2, 6, 12, 24, 30, 42, 56
241230422Option A
The series is , (1^2 + 1), (2^2 + 2), (3^2 + 3)… - 1, 6, 24, 60, 120, 210
616024210Option B
The series is, (1^3 – 1), (2^3 – 2), (3^3 – 3), (4^3 – 4)…
21
Mixed Quantitative Aptitude Questions Set 238
- Directions : What will come in place of questions marks (?) in the following questions ? ( You are not to calculate the exact value )
(20.24% of 749.81) ÷ 2.89 + 85.20 = ?125135120130145Option B
20% of 750/3 + 85 = ?
? = 135 - (12.138 * 4 + 4.98 * 7.99) ÷ ( 9.12 + 1.85) = ?
5681215Option C
( 12 * 4 + 5 * 8) ÷ 9 + 2 = ?
? = 88/11
? = 8 - √100.12 – √63.87 + √144.01 * 5.32 = ?
5882946252Option D
10 – 8 + 12 * 5 = ?
? = 62 - (34.07)^2 + (15.89)^2 -√576.02 + 45.88 = ?
15201430143413341324Option C
1156 + 256 – 24 + 46 = ?
? = 1434 - 449. 75 ÷ 8.82 + 19.95 * 3.22 + √675.82 = ?
152183130136120Option D
450 ÷ 9 + 20 * 3 + √676 = ?
? = 50 + 60 + 26
? = 136
12, 13, 24, 72, 288, 1440121314402472Option B
The series is, * 1, * 2, * 3 …- 520, 525, 540, 585, 720, 1120
5257201120720585Option C
The series is, + 5, + 15, + 45, + 135, + 405 - 185, 166, 189, 160, 191, 156
185189160156166Option D
The series is, -19, + 23, -29, + 31, -33 - 9, 12, 27, 84, 339, 1544
339842791544Option E
The series is, (* 1 + 3), (* 2 + 3), (* 3 + 3)… - 325, 329, 340, 354, 379, 415
329379354340415Option D
The series is, + 4, + 9, + 16, + 25, + 36
Directions : What will be wrong number in the given wrong number series ?
22
Mixed Quantitative Aptitude Questions Set 237
- A starts a business with rs.4000 and B joins him after 3 months with rs. 16000. If total profit of the business is rs.2000, then find profit share of B.
2000100012008501500Option E
Profit sharing ratio of A and B = (4000 * 12) : (16000 * 9)
= 48 : 144 = 1 : 3
profit share of B = 2000 * 3/4 = 1500 - The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio ?
5 : 318 : 1921 : 223 : 85 : 4Option C
Let number of boys and girls are 7x and 8x respectively
ratio after increased =
7x * 6/5 : 8x * 11/10 = 21 : 22 - The ratio between the present ages of P and Q is 5 : 7 respectively. If the difference between Q’s present age and P’s age after 6 years is 2 what is the total P’s and Q’s present age ?
32 years68 years50 years48 years26 yearsOption D
Let present age of P and Q = 5x and 7x
7x – (5x + 6) = 2
x = 4
total = 12x = 12 * 4 = 48 years - The ratio of milk to water in total 56 liter of mixture is 5 : 3. If ‘x’ liter of milk and water is added in the mixture so that ratio becomes 25 : 18, then find the value of ‘x’.
20 liters12 liters18 liters15 liters22 litersOption D
Quantity of milk in the mixture = 56 * 5/8 = 35
water = 56 * 3/8 = 21
35 + x/21 + x = 25/18
x = 15 liter - 4 kg of rice at rs.8 per kg is mixed with 8 kg of wheat at rs.12 per kg. What is the average price of the mixture ?
1210.665812Option B
Total cost of 4 kg rice = 4 * 8 = 32
total cost of 8 kg wheat = 8 * 12 = 96
average = 128/12 = 10.66 - Directions : What will come in place of questions marks (?) in the following questions given below ?
15% of 220 + 20 * 15 – √1156 = ?320300284299340Option D
33 + 300 – 34 = ?
? = 299 - 3240 – 2240 + 2050 – 1800 = ?
20301250314012401350Option B
? = 5290 – 4040
? = 1250 - √1296 – 30% of 120 + 40 + ? = 188
152320145148200Option D
36 – 36 + 40 + ? = 188
? = 148 - (18)^2 – (12)^2 + 420 – 120 = ?
320126440480520Option D
324 – 144 + 420 – 120 = ?
? = 480 - (15)^2 – 30 * 8 + (40)^2 = ?
14851575134015851235Option D
225 – 240 + 1600 = ?
? = 1585
23
Mixed Quantitative Aptitude Questions Set 236
- Directions : In the following questions, two equations I and II are given. You have to solve the equations and give answer the questions.
I. x^2 + 13x + 42 = 0
II. y^2 + 8y + 12 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption D
I. x^2 + 7x + 6x + 42 = 0
x = -7, -6
II. y^2 + 6y + 2y + 12 = 0
y = -6, -2 - I. x^3 = 2744
II. y^2 = 289X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. x^3 = 2744
x = 14
II. y^2 = 289
y = 17, -17 - I. x^2 – 2x – 24 = 0
II. y^2 + 3y – 40 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. x^2 – 6x + 4x – 24 = 0
x = 6, -4
II. y^2 + 8y – 5y – 40 = 0
y = -8, 5 - I. 2x^2 + 10x + 12 = 0
II. y^2 + 10y + 25 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption A
I. 2x^2 + 6x + 4x + 12 = 0
x = -3, -2
II. y^2 + 5y + 5y + 25 = 0
y = -5, -5 - I. (x – 2)^2 = x – 2
II. y^2 – 14y + 48 = 0
X > YX < YX ≥ YX ≤ YX = Y or no relationOption B
I. (x – 2)^2 = x – 2
x^2 – 4x + 4 = x – 2
x^2 – 5x + 6 = 0
x^2 – 3x – 2x + 6 = 0
x = 3, 2
II. y^2 – 8y – 6y + 48 = 0
y = 8, 6 - Directions : What will come in place of questions mark (?) in the following questions below ?
36% of 1800 + 80% 495 – (8)^2 = ?9708804409801020Option D
648 + 396 – 64 = ?
? = 980 - 12 * ? + (10)^2 = (16)^2 – 10 * 6
5821412Option B
12 * ? + 100 = 256 – 60
12 * ? = 196 – 100
? = 8 - 32 * 3 + 60% of 300 = (?) + √400
1415121624Option D
96 + 180 = (?)^2 + 20
(?)^2 = 256
? = 16 - 264 ÷ 24 + 190 ÷ 5 = ? ÷ 5
245315255320240Option A
264/24 + 190/5 = ?/5
? = (11 + 38) * 5
? = 245 - ?/27 * 60 = 12 * 3 * 5/?
520620440540480Option D
(?)^2 = 12 * 3 * 5 * 27 * 60
(?)^2 = 36 * 5 * 9 * 3 * 12 * 5
? = √(36 * 25 * 9 * 36 )
? = 36 * 5 * 3
? = 540
24
Mixed Quantitative Aptitude Questions Set 235
- 6 men or 8 women or 3 boys completed certain work in a day is equal. Find in how many days a man and a boy can complete the three-fourth of same work together ?
2 days3 days5 days6 days1.5 daysOption E
Let total work = 48
6 men = 8men = 3 boys
efficiency of a man = 48/6 = 8
efficiency of a woman = 48/8 = 6
efficiency of a boy = 48/3 = 16
days require = 48/(16 + 8) * 3/4 = 1.5 days - A sum becomes rs.9280 in 6 years and becomes rs.10440 in 8 days at the same rate on simple interest. Find compound interest earned in 2 years on rs.6000 at same rate of interest ?
15201840254013401260Option E
SI for 2 years = 10440 – 9280 = 1160
SI for 6 years = 1160/2 * 6 = 3480
sum = 9280 – 3480 = 5800
rate interest = 3480/(5800 * 6) *100 = 10%
CI for 2 years = 10 + 10 + 10 * 10/100 = 21%
CI = 6000 * 21/100 = 1260 - A bat was sold at rs,1260 after giving 30% discount on market price. If discount was not given, then he would have earned 50% profit. Find cost price of bat ?
14001280180012001440Option D
Market price of bat = 1260/70 * 100 = 1800
CP = 1800/150 * 100 = 1200 - Two trains travel from Mumbai to Bangalore and Bangalore to Mumbai in 10 hours and 12 hours respectively. Both trains started simultaneously at 8 am and the train started from Mumbai met with accident at 12 pm. Find percentage reduction in speed of train started from Mumbai, if they meet each other at 2 pm, assume there is no loss of time in accident ?
30%48%50%42%20%Option C
Ratio of speed is inversely proportional to time taken if distance is constant.
Let speed of Mumbai to Bangalore travelling train = 6x km/hr
speed of Bangalore to Mumbai travelling train = 5x km/hr
Let total distance = 60x km
let speed of train after accident = y km/hr
60x = 4 (6x + 5x) + 2 (y + 5x)
y = 3x km/hr
reduction in speed = 6x – 3x/6x * 100 = 50% - The radius of a circle is 14 km. What is area of another circle having radius 1.5 times of the actual circle ?
1540 cm^21386 cm^21440 cm^21450 cm^21240 cm^2Option B
Radius of another circle = 14 * 1.5 = 21 cm
area = πr^2 = 22/7 * 21 * 21 = 1386 cm^2 - Directions : What will come in place of questions (?) mark in the following missing series ?
4, 2, 3, 7.5, 26.25, ?120.125118.5114.5118.125120Option D
The series is, (* .5), (* 1.5), (* 2.5), (* 3.5), (* 4.5) - 148, 196, 268, 364, 484, ?
650640452620628Option E
The series is, (+ 48), (+ 72), (+ 96), (+ 120), (+ 144), - 46, 52, ?, 136, 256, 466
8478687680Option D
The series is, (+ 2^3 – 2), (+ 3^3 – 3), (+ 4^3 – 4), (+ 5^3 – 5), (+ 6^3 – 6), - 16000, 8000, 24000, 6000, ?, 30000, 5000
4000018000120004200030000Option E
The series is, (÷ 2), (* 3), (÷ 4), (* 5), (÷ 6) - 24, 28, 36, 52, 84, ?
240148120124168Option B
The series is, (+ 4), (+ 8), (+ 12), (+ 32), (+ 64),
25
Mixed Quantitative Aptitude Questions Set 234
- 6 men or 8 women or 3 boys completed certain work in a day is equal. Find in how many days a man and a boy can complete the three-fourth of same work together ?
2 days3 days5 days6 days1.5 daysOption E
Let total work = 48
6 men = 8men = 3 boys
efficiency of a man = 48/6 = 8
efficiency of a woman = 48/8 = 6
efficiency of a boy = 48/3 = 16
days require = 48/(16 + 8) * 3/4 = 1.5 days - A sum becomes rs.9280 in 6 years and becomes rs.10440 in 8 days at the same rate on simple interest. Find compound interest earned in 2 years on rs.6000 at same rate of interest ?
15201840254013401260Option E
SI for 2 years = 10440 – 9280 = 1160
SI for 6 years = 1160/2 * 6 = 3480
sum = 9280 – 3480 = 5800
rate interest = 3480/(5800 * 6) *100 = 10%
CI for 2 years = 10 + 10 + 10 * 10/100 = 21%
CI = 6000 * 21/100 = 1260 - A bat was sold at rs,1260 after giving 30% discount on market price. If discount was not given, then he would have earned 50% profit. Find cost price of bat ?
14001280180012001440Option D
Market price of bat = 1260/70 * 100 = 1800
CP = 1800/150 * 100 = 1200 - Two trains travel from Mumbai to Bangalore and Bangalore to Mumbai in 10 hours and 12 hours respectively. Both trains started simultaneously at 8 am and the train started from Mumbai met with accident at 12 pm. Find percentage reduction in speed of train started from Mumbai, if they meet each other at 2 pm, assume there is no loss of time in accident ?
30%48%50%42%20%Option C
Ratio of speed is inversely proportional to time taken if distance is constant.
Let speed of Mumbai to Bangalore travelling train = 6x km/hr
speed of Bangalore to Mumbai travelling train = 5x km/hr
Let total distance = 60x km
let speed of train after accident = y km/hr
60x = 4 (6x + 5x) + 2 (y + 5x)
y = 3x km/hr
reduction in speed = 6x – 3x/6x * 100 = 50% - The radius of a circle is 14 km. What is area of another circle having radius 1.5 times of the actual circle ?
1540 cm^21386 cm^21440 cm^21450 cm^21240 cm^2Option B
Radius of another circle = 14 * 1.5 = 21 cm
area = πr^2 = 22/7 * 21 * 21 = 1386 cm^2 - Directions : What will come in place of questions (?) mark in the following missing series ?
4, 2, 3, 7.5, 26.25, ?120.125118.5114.5118.125120Option D
The series is, (* .5), (* 1.5), (* 2.5), (* 3.5), (* 4.5) - 148, 196, 268, 364, 484, ?
650640452620628Option E
The series is, (+ 48), (+ 72), (+ 96), (+ 120), (+ 144), - 46, 52, ?, 136, 256, 466
8478687680Option D
The series is, (+ 2^3 – 2), (+ 3^3 – 3), (+ 4^3 – 4), (+ 5^3 – 5), (+ 6^3 – 6), - 16000, 8000, 24000, 6000, ?, 30000, 5000
4000018000120004200030000Option E
The series is, (÷ 2), (* 3), (÷ 4), (* 5), (÷ 6) - 24, 28, 36, 52, 84, ?
240148120124168Option B
The series is, (+ 4), (+ 8), (+ 12), (+ 32), (+ 64),
26
Mixed Quantitative Aptitude Questions Set 233
- A container which contains 80 liters of milk and water in the ratio of 3 : 2. How much quantity of mixture should be replaced with water so that in the final mixture, ratio of milk to water is 9 : 11 ?
25 liters32 liters28 liters20 liters42 litersOption D
Quantity of milk = 80 * 3 /5 = 48 liters
Quantity of water = 80 * 2 /5 = 32 liters
let ‘x’ liters of mixture is replaced with water.
(48 – x * 3/5 ) / (32 – x * 2/5 + x) = 9/11
x = 20 liters - Ram bought a chair for rs.480 and marked is at rs.720. If he made a profit of 25% on selling the table then find percentage discount allowed by Ram on the chair ?
15%20%18%45%16.67%Option E
SP of chair = 480 * 125/100 = 600
MP = 720
discount percentage = 720 – 600/720 * 100 = 16.67% - A alone can do a work in 25 days whereas B and C together can do some work in 20 days. A and B together worked for 8 days then A left the work. If efficiency of C is half of efficiency of A, then in how many days remaining work will be completed b A and C together ?
5 days7 1/3 days15 days8 days14 daysOption B
LCM of 25 and 20 = 100
efficiency of A = 100/25 = 4
efficiency of B and C = 100/20 = 5
efficiency of C = 4/2 =2
efficiency of B = 5 – 2= 2
A and B worked for 8 days = 8 ( 4 + 3) = 56 work
remaining work = 100 – 56 = 44
remaining work will be completed A and C together = 44/4 + 2 = 7 1/3 days - Train A travelling at 72 km/hr crosses a platform of 160 m in 18 seconds and train B travelling at 90 km/hr crosses the same platform in 15 seconds. Find the length of train B ?
320m240m210m225m215mOption E
Speed of train A = 72 * 5/18 = 20 m/sec
distance covered by train A = 20 * 18 = 360 m
length of train A = 360 – 160 = 200m
speed of train B = 90 * 5/18 = 25 m/sec
distance covered by train B = 25 * 15 = 375 m
length of train B = 375 – 160 = 215 m - A is 6 years younger than B and ratio of present age of B to C is 12 : 5. If ratio of present age of A to C is 2 : 1, then find present age of B ?
32 years34 years42 years36 years40 yearsOption D
Let present age of B = 12x
age of C = 5x
age of A = 12x – 6
12x – 6/5x = 2/1
12x – 6 = 10x
2x = 6
x = 3
present age of B = 12 * 3 = 36 years - Directions : What will come in place of questions marks ( ? ) in the following questions below ?
35% of 320 + 440 – √1024 = ?540320340620520Option E
112 + 440 – 32 = ?
? = 520 - 124 * 4 – 320 ÷ 5 + √361 – 18 = ?
225320435433520Option D
496 – 64 + 19 – 18 = ?
? = 433 - 495 ÷ 5 + (21)^2 – (20)^2 = ?
324420325140260Option D
99 + 441 – 400 = ?
? = 140 - 1240 + 2520 – 3540 + 4250 = ?
43405470424034504470Option E
? = 8010 – 3540
? = 4470 - (12)^2 + (18)^2 – (20)^2 + (14)^2 = ?
365264345420540Option B
144 + 324 + 196 – 400 = ?
? = 264
27
Mixed Quantitative Aptitude Questions Set 232
- The ratio of the milk to water in a mixture is 4 : 3. 21 liter of mixture is taken out and 8 liter of milk and 14 liter of water is added in mixture, so that new ratio of milk to water becomes 320 : 17, then find initial quantity of milk in the mixture ?
84 liters35 liters63 liters80 liters72 litersOption A
Let quantity of milk and water in the mixture = 4x and 3x respectively
(4x – 21 * 4/7 + 8)/(3x – 21 * 3/7 + 14) = 20/17
4x – 4/3x + 5 = 20/17
x = 21
Initial quantity of milk in the mixture = 4x = 4 * 21 = 84 liters - A alone can do 40% of work in 8 days and B alone can do 30% of work in 12 days. If efficiency of C is 50% more than A, then find in how many days A, B and C together will be completed 90% of work ?
5 days8 days12 days6 days4 daysOption D
Total days required to complete the work by A = 8/40 * 100 = 20
total days required to complete the work by B = 12/30 * 100 = 40
LCM of 20 and 40 = 40
efficiency of A = 40/20 = 2
efficiency of B = 40/40 = 1
efficiency of C = 2 * 150/100 = 3
days required = 40/6 * 90/100 = 6 days - The ratio of present age of A and B is 3 : 4. If the ratio of age of A after 6 years and age of B before 4 years is 6 : 5, then find the age of B after 4 years ?
42 years25 years26 years28 years40 yearsOption D
Let the present age of A and B = 3x and 4x
3x + 6/ 4x – 4 = 6/5
15x + 30 = 24x – 24
x = 6
the age of B after 4 years = 4x + 4 = 28 years - A man goes from a place A to B at a speed of 12 km/hr and returns from B to A at a speed of 18 km/hr. What is the average speed for the whole journey ?
12 km/hr24 km/hr14 km/hr14 2/5 km/hr15 2/5 km/hrOption D
Average speed = 2xy /x + y
= 2 * 12 * 18/12 + 18 = 14 2/5 km/hr - A boat covers 12 km upstream and 18 km downstream in 3 hours while it covers 36 km upstream and 24 downstream in 6 1/2 hours, what is the speed of stream ?
5 km/hr4 km/hr6 km/hr2 km/hr8 km/hrOption D
12/x – y + 18/x + y = 3
36/x – y + 24/x + y = 13/2
let x – y = a, x + y = b
12/a + 18/b = 3
36a + 24/b = 13/2
By multiplying ‘3’ in equation (i)
36/a + 54/b = 9
36/a + 24/b = 13/2
30/b = 9 – 13/2
b = 12
36/a + 9/2 = 9
36/a = 9/2
a = 8
x – y = 8
x + y = 12
2x = 20
x = 10
y = 2 - Directions : What will come in place of questions marks (?) in the following number series ?
345, 358, 375, ?, 417, 446380382392394396Option D
The series is, (+ 13), (+ 17), (+ 19), (+ 23), (+ 29), - 5, 11, 35, 143, 719, ?
42404319446549784565Option B
The series is, ( * 2 + 1), ( * 3 + 2), ( * 4 + 3), ( * 5 + 4), ( * 6 + 5), - 20, 18, 38, 56, 94, ?
155100120125150Option E
The series is, (20 + 18), (18 + 56), (56 + 94) - 35, 40, 55, 80, 115, ?
145180160172165Option C
The series is, (+ 5), (+ 15), (+ 25), (+ 35), (+ 45), - 35, 18, 19, 30, ?, 157.5
6462589686Option B
The series is, ( * 5 + .5), (* 1 + 1), (* 1.5 + 1.5), (* 2 + 2), (* 2.5 + 2.5)
28
Mixed Quantitative Aptitude Questions Set 231
- I. x^2 – 11x + 18 = 0
II. y^2 – 16 y + 39 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. x^2 – 9x – 2x + 18 = 0
x = 9, 2
II. y^2 – 13y – 3y + 39 = 0
y = 13, 3 - I. 2x^2 + 19x + 35 = 0
II. 2y^2 + 7y + 5 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption D
I. 2x^2 + 14x + 5x + 35 = 0
2x = -14, – 5
x = -7, -2.5
II. 2y^2 + 5y + 2y + 5 = 0
2 = -5, -2
y = -2.5, -1 - I. x^3 = 512
II. y^2 – 13y + 40 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption C
I. x^3 = 512
x = 8
II. y^2 – 8y – 5y + 40 = 0
y = 8, 5 - I. (x – 4)^2 = 0
II. 2y^2 – 5y + 2 = 0X > YX < YX ≥ YX ≤ YX = Y or no relationOption A
I. x^2 – 4x – 4x + 16 = 0
x = 4, 4
II. 2y^2 – 4y – y + 2 = 0
y = 2, .5 - I. x^4 = 1296
II. y^3 = 216X > YX < YX ≥ YX ≤ YX = Y or no relationOption E
I. x^4 = 1296
x = 6
II. y^3 = 216
y = 6 - Directions : What will come in place of questions (?) marks in the following questions given below ?
21 * 25 – (8)^3 + (16)^2 – ? = (17)^22522386420Option E
525 – 512 + 256 + ? = (17)^2
269 + ? = 289
? = 20 - 672 ÷ 28 + 22 * 19 – (15)^2 = ?
218256320217215Option D
24 + 418 – 225 = ?
? = 217 - 55% of 320 + √? = 16 * 8 + 84
3684216129626Option D
176 + √? = 212
√? = 36
? = 1296 - √2025 ÷ 9 * 4 + 25 of 20 ÷ 4 = ?
120132138145136Option D
45 ÷ 9 * 4 + 25 * 20/4 = ?
? = 20 + 125
? = 145 - (?)^3 ÷ 180 = 1200
2562656036Option D
(?)^3 = 1200 * 180
? = 60
29
Mixed Quantitative Aptitude Questions Set 230
- P is 25% more efficient than Q and he completes a task in 36 days. If R alone complete the same task in 30 days, then find all three together can complete the same task in how many days ?
15 days18 days8 days14 days12 daysOption E
Ratio of efficiency of A and B = 5 : 4
total work = 36 * 5 = 180
efficiency of C = 180/30 = 6
required time = 180/5 + 4 + 6 = 12 days - A shopkeeper marked up an article 60% above cost price and sell it at rs.960 after allowing discount of 25%. If profit of shopkeeper is rs.160, then find the marked price of article ?
14201200114015401280Option E
Let CP of article = 100x
MP of article = 160x
CP = 960 – 160 = 800
100x = 800
x = 8
MP of article = 160 * 8 = 1280 - Average of serious of six consecutive even numbers is 25, find the sum of second and fourth number of serious.
4335244856Option D
Let series be x, x + 2 , x + 4, x + 6, x + 8, x + 10
6x + 30/6 = 25
x = 20
2nd and 4th number = (20 + 2 = 22), ( 20 + 6 = 26)
sum = 48 - Ratio of investment of A, B and C is 4 : 6 : 9 respectively. At the end of a year, ratio of profit share of A, B and C is 4 : 5 : 6 respectively. If A has invested for a year then find the sum of period of investment of B and C ?
20 months18 months14 months24 months28 monthsOption B
Let investment of A, B and C = 4x, 6x and 9x respectively
period of investment of B and C = a and b months respectively.
ratio of profit share ,
A : B : C = 4x * 12 : 6x * a : 9x * b
4x * 12/6x * a = 4/5
a = 10 months
4x * 12/9x * b = 4/6
b = 8 months
required sum = 10 + 8 = 18 months - Ratio between income and expenditure of Sujit increased by 20% and 33.33% in two successive years and expenditure remains same, then his saving is increased by rs.18000. What is his new income ?
4500038000650003200048000Option E
Income and expenditure of Sujit 15x and 6x respectively.
saving = 15x – 6x = 9x
new income = 15x * 6/5 * 4/5 = 24x
24x – 6x = 9x + 18000
x = 2000
new income = 24 * 2000 = 48000 - Directions : What will come in place of questions (?) marks in the following number series ?
36, 18, ?, 27, 54, 1351219201822Option D
The series is, (* .5), (* 1), (* 1.5), (* 2), (* 2.5) - 26, 170, 366, 622, ? 1346
834946870650820Option B
The series is, (+ 12)^2, (+ 14)^2, (+ 16)^2, (+ 18)^2, (+ 20)^2 - 10, 11, 15, 24, ? 65
4530384045Option D
The series is, (+ 1)^2, (+ 2)^2, (+ 3)^2, (+ 4)^2, (+ 5)^2, - 8, 16, 43, 168, 511, ?
14521234102018422024Option D
The series is, (+ 2)^3, (+ 3)^3, (+ 5)^3, (+ 7)^3, (+ 11)^3, - 2, 5, 12, 27, 58, ?
124240234121320Option D
The series is, (* 2 + 1), (* 2 + 2), (* 2 + 3), (* 2 + 4), (* 2 + 5),
30
Mixed Quantitative Aptitude Questions Set 229
- 375 ml of mixture contains milk and water in the ratio of 16 : 9 respectively. If x ml of water is added into the mixture then the ratio of milk to water in the resultant mixture becomes 3 : 2, find the value x.
3025354045Option B
Quantity of milk = 375 * 16/25 = 240
quantity of water = 375 * 9/25 = 135
ATQ,
240/135 + x = 3/2
3x + 405 = 480
x = 25 - A and B alone can complete a piece of work in 24 days and 20 days respectively. If efficiency of C is 60% more than A, then find in how many days C complete the work ?
15 days17 days20 days25 days30 daysOption A
LCM of 24 and 20 = 120
efficiency of A = 120/24 = 5
efficiency of B = 120/20 = 6
efficiency of C = 5 * 160/100 = 8
time required = 120/8 = 15 days - A shopkeeper marked up an article 25% above its cost price and allowed a discount of 40% on it. If shopkeeper made a loss of rs.128, then find what is the cost price ?
620340580512480Option D
Let CP of article = 100x
MP of article = 100x * 125/100 = 125x
SP of article = 125x * 60/100 = 75x
loss = 100x – 75x = 25x
CP of article = 128/25x * 100x = 512 - P and Q started a partnership business with investment of rs.15000 and rs.12000 for 8 months and 6 months respectively. If total profit of the business is 6400, then what is profit share of P ?
32004450380042004000Option E
Profit sharing ratio of P and Q = 15000 * 8 : 12000 * 6 = 5 : 3
profit share of P = 6400 * 5/8 = 4000 - A man invested rs. 25000 at the rate of 20% in compound interest for 1 year. How much amount he received if he invested for compounded half yearly.
4200022000302502814034400Option C
Rate of compound interest for half yearly = 20/2 = 10%
rate of CI after 1 year = 10 + 10 + 10 * 10/100 = 21%
CI = 25000 * 21/100 = 5250
amount = 25000 + 5250 = 30250 - Directions : What will come in place of questions mark in the following questions given below ?
20^2 + 328 – 84 = 28% of 300 + ?
320480340610560Option E
400 + 328 – 84 = 84 + ?
? = 560 - √1156 + 12^2 – 19 * 5 = ?
8284839293Option C
34 + 144 – 95 = ?
? = 83 - 42% of 800 + 120% of 1400 – 520 = ?
32001496144512962050Option B
336 + 1680 – 520 = ?
? = 1496 - 450/3 + 320 – 210 + 150 = ?
520440420450410Option E
150 + 320 + 150 – 210 = ?
? = 410 - 350 ÷ 7 of 25 + 340 + (12)^2 = ?
328486284320325Option B
350 /(7 * 25) + 340 + 144 = ?
? = 486
31
Mixed Quantitative Aptitude Questions Set 228
- 4 men or 8 women can do a work in 15 days, then in how many days 6 men and 12 women can complete the whole work ?
4 days3 days5 days6 days8 daysOption C
Efficiency ratio of men and women = 2 : 1
total work = 4 * 2 * 15 = 120
days required = 120/ 6 * 2 + 12 * 1 = 5 days - If simple interest earned on a certain sum of money at certain rate of interest after 5 years is 2/7 times the amount earned on the same sum of money after 5 years, then what is the rate interest ?
10%6%12%8%15%Option D
Let amount = 7x
SI = 2x
P = 7x – 2x = 5x
rate of interest = 2x * 100/5x * 5 = 8% - Average of 12 numbers is 60. If average of first six and last four numbers is 70 and 50 respectively and ratio of seventh and eighth number is 3 : 2, then find the 8th number ?
5040807075Option B
Total 12 numbers = 12 * 60 = 720
total of first six numbers = 70 * 6 = 420
total of last four numbers = 50 * 4 = 200
8th number = (720 – 420 + 200) 2/5 = 100 * 2/5 = 40 - Sanjay saves 25% of his monthly income. If his monthly expenditure is increased by 40% while his monthly savings remain same, then find the percentage increase in his monthly income ?
36%40%28%30%40%Option D
Let income of Sanjay = 100x
savings = 100x * 25/100 = 25x
expenditure = 100x – 25x = 75x
increased expenditure = 75x * 140/100 = 105x
income = 105x + 25x = 130x
% increased income = 130x – 100x/100 * 100 = 30% - 490 ml of mixture contains milk and water in the ratio of 4 : 3 respectively. If 140 ml of mixture is taken out and 50 ml of water is added, then what is the ratio of milk to water in final mixture ?
2 : 34 : 53 : 21 : 12 : 5Option D
Quantity of milk = 490 * 4/7 = 280
quantity of water = 490 * 3/7 = 210
140 ml of mixture is taken out,
(280 – 140 * 4/7)/(210 – 140 * 3/7 + 50) = 200/200 = 1 : 1 - Directions : What will come in place of questions marks (?) in the following given number series ?
30, 62, 126, 254, 510, ?92010226488401220Option B
The series is (*2 + 2), (*2 + 2), (*2 + 2)… - ?, 9, 25, 61, 125, 225
54682Option A
The series is (+2^2), (+4^2), (+6^2), (+8^2), (+10^2) - 35, 42, 56, 77, ?, 140
135140130105112Option D
The series is (+7), (+14), (+21), (+28), (+35) - 8, 16, 48, 192, 960, ?
48205760192032009600Option B
The series is (*2), (*3), (*4), (*5), (*6) - 320, 330, 350, 385, 430, ?
320520640510650Option D
The series is difference of difference.
32
Mixed Quantitative Aptitude Questions Set 227
- A, B and C entered into a partnership business and A gets profit rs.960 out of total profit rs.5120. C invested rs.14000 for 8 months and B invested rs. 8000. If A invested rs.4000 more than that of B and 4 months less that of C, then find what is the profit share of C ?
21201345124022401050Option D
Investment of A = 8000 + 4000 = 12000
time period for investment of A = 8 – 4 = 4months
profit sharing ratio of A, B and C = (12000 * 4) : (8000 * 12) : (14000 * 8) = 3 : 6 : 7
profit share of C = 5120 * 7/16 = 2240 - Amit invested rs.22500 in scheme X offering 10% compound interest for 2 years. If he invested 40% of the money received by him from scheme X in another scheme Y offering 20% simple interest for 4 years, then how much amount received by him from scheme Y ?
1234038450196022050523420Option C
CI received after 2 years = 22500 * 10/100 * 10/100 = 4725
total amount = 22500 + 4725 = 27225
40 % of 27225 = 10890
SI received after 4 years = 27225 * 40/100 * 4 * 20/100 = 8712
total amount = 10890 + 8712 = 19602 - The monthly income of A is rs.28000 and he saves 28 4/7% of his monthly income. If the monthly expenditure of B is rs.4000 more than A and also expenditure of B is 20% less than his income, then find saving of B is how much percent more or less than savings of A ?
20%30%15%25%22%Option D
Income of A = 28000
savings of A = 28000 * 2/7 = 8000
expenditure of A = 28000 – 8000 = 20000
expenditure of B = 20000 + 4000 = 24000
income of B = 24000/4 * 5 = 30000
saving of B = 30000 – 24000 = 6000
% less = 8000 – 6000/8000 * 100 = 25% - The ratio of male to female in a company is 5 : 3 and the number of male in the company is 1250. If the number of female and male is increased by 10% and 8% respectively, then find what percent change in total population ?
5.2%6%8%7.25%8.75%Option E
The number of male = 1250
the number of female = 1250/5 * 3 = 750
the number of male after increased = 1250 * 108/100 = 1350
the number of female after increased = 750 * 110/100 = 825
total population = 1250 + 750 = 2000
total population after increased = 1350 + 825 = 2175
change in population = 2175 – 2000/2000 = 8.75% - A man travels 150 km to a place in 3 hours 20 minutes and he returns to the starting point in 4 hours 10 minutes. Let x be the rate for the entire trip. Then in how many kilometers per hour more or less than x ?
4 km/hr2 km/hr4.5 km/hr5 km/hr8 km/hrOption D
Time taken to cover 150 km in going trip
3 hours 20 minutes = 3 20/60 = 3 1/3 hours
speed in going trip = 150 *3/10 = 45 km/hr
time taken to cover 150 km in return trip = 4 hours 10 minutes = 4 1/6 hours
speed in return trip = 150 * 6/25 = 36 km/hr
average speed = 2 * 45 * 36/ 45 + 36 = 40 km/hr
required difference = 45 – 40 = 5 km/hr - Direction : What will come in place of question(?) mark in the following questions given below ?
60% of 1800 + 24% of 3500 – 32% of 150 = ?19921872209215321240Option B
1080 + 840 – 48 = ?
? = 1872 - 3/5 * 4/7 * 5/12 * 1015 = ?
1201451678952Option B
? = 3/5 * 4/7 * 5/12 * 1015
? = 145 - 4545 + 4320 – 2540 + 320 = ?
36422720452066453435Option D
4545 + 4320 + 320 – 2540 = ?
? = 6645 - 330 – 345 + 421 – 22% of 1500 = ?
7632455265Option A
330 + 421 – 345 – 330 = ?
? = 76 - 552 ÷ 24 * 5 + 113 – 85 = ?
144143320245145Option B
23 * 5 + 113 – 85 = ?
? = 143
33
Mixed Quantitative Aptitude Questions Set 226
- A shopkeeper X sold an article for rs.850 at a profit of 25%. Another shopkeeper Y sold the another article and earned 30% more profit than the profit earned by X. If the selling price of article Y is three-fifth of selling price of article X, then find the profit percent of article Y ?
64 2/17%76 8/17%52 3/34%52 3/8%78%Option B
SP of article X = 850
CP of article X = 850 * 100/125 = 680
profit = 170
profit of article Y = 170*130/100 = 221
SP of article Y = 850 * 3/5 = 510
CP = 510 – 221 = 289
profit percent = 221/289* 100 = 76 8/17% - Mixture A contains milk and water in the ratio of 3 : 2 respectively, while mixture B contains water and milk in the ratio of 4 : 3 respectively. If the quantity of water in mixture B is twice the quantity of water in mixture A, then find the quantity of milk in mixture A is what percent quantity of water in mixture B ?
68%60%82%75%56%Option D
Quantity of milk and water in mixture A = 3x and 2x
according to questions,
quantity of water in mixture B = 2*2x = 4x
quantity of milk in mixture B = 4x/4 *3 = 3x
required percentage = 3x/4x*100 = 75% - 340 liters of mixture of milk and water is contained in a container having milk and water mixed in the ratio of 3 : 1 respectively. 76 liters of this mixture is taken out from the container and replaced with (x + 7) liters of milk so that the ratio of water to milk is 6 : 11. What is the value of ‘x’ ?
4248383552Option D
Quantity of milk in the container = 340 * 3/4 = 255
quantity of water in the container = 340*1/4 = 85
76 liters of mixture is taken out and (x + 7) liter of water is added.
(255 – 57) / 85 – 19 + (x + 7) = 11/6
198/(73 + x) = 11/6
11x = 385
x = 35 - A can do a piece of work in 30days while B and C together can complete the work in 20 days and A and C together can complete the work in 24 days. If B is worked in two-fifth of his efficiency, then in how many days A and B together complete half of the work ?
8 days6 days8 1/3 days5 days10 daysOption E
LCM of 30 , 20 and 24 = 120
efficiency of A = 120/30 = 4
efficiency of B and C = 120/20 = 6
efficiency of A and C together = 120/24 = 5
efficiency of C = 5- 4 = 1
efficiency of B 6- 1 = 5
two-fifth of efficiency B = 5 * 2/5 = 2
time required to complete half of the work = 60/2 + 4 = 10 days - Rohan and Sivan started a business together with initial investments of rs. 1500 and rs.1800 respectively. If after 2.5 years profit share of Rohan and Sivan are rs(x + 80) and (x + 120) respectively, then find the difference between profit of Rohan and Sivan ?
180120320130340Option B
Profit sharing ratio of Rohan and Sivan = (1500 * 2.5) : (1800 * 2.5) = 5 : 6
x + 80/x + 120 = 5/6
6x + 480 = 5x + 600
x = 120 - Directions : In each of these questions given below two equations. You have to solve both the equations and give answer.
I. x^2 – 7√3 + 36 = 0
II. y^2 – 6√2 + 16 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 – 4√3 – 3√3 + 36 = 0
x = 4√3 , 3√3
II. y^2 – 4√2 – 2√2 + 16 = 0
y = 4√2, 2√2 - I. x^2 + √2x – 12 = 0
II. y^2 – 8√3 + 48 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option B
I. x^2 + 3√2 – 2√2 – 12 = 0
x = -3√2, 2√2
II. y^2 – 4√3 – 4√3 + 48 = 0
y = 4√3, 4√3 - I. x^2 – 36 = 0
II. y^2 – 15y + 36 = 0
X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 = 36
x = 6, -6
II. y^2 – 12y – 3y + 36 = 0
y = 12, 3 - I. y^2 = 144
II. 2x^2 – 12x + 16 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. y^2 = 144
y = 12, -12
II. 2x^2 – 8x – 4x + 16 = 0
2x = 8, 4
x = 4, 2 - I. x^2 – 2x – 195 = 0
II. y^2 – 24y + 128 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 – 15x + 13x – 195 = 0
x = 15, -13
II. y^2 – 16y – 8y + 128 = 0
y = 16, 8
34
Mixed Quantitative Aptitude Questions Set 225
- What is the monthly income of Jitu ?
I. Jitu spends 85% of his income on various expenses and remaining amount he saved.
II. Monthly saving of Jitu are rs.7500.
III. Out of total money spent by Jitu in a month, one-fifth is spent on rent and remaining amount of rs.34000 on other items.Only I and II sufficientOnly II and III sufficientOnly I and II sufficientNeither I nor II and III is sufficientAny of the two statements is sufficientOption E
Let income of Jitu = rs.x
from I and II,
15% of x = 7500
x = 7500 * 100/15 = 50000
From I and III,
x * 85/100 * 4/5 = 34000
x = 50000
from I and III
4/5 th of expenditure = 34000
expenditure = 42500
income = 42500 + 7500 = 50000
thus, answer can be find out by any of two given statement - How much time will require the train to reach from point X to point Y ?
I. The train will pass the other train of equal length of 400m running opposite in direction in 16 secs
II. Distance between point X and Y is 252 km.
III. The 400m long train crosses a signal pole in 20sec.Only I and II is sufficientOnly II and III is sufficientNeither of any statement is sufficientAll statements are sufficientOnly I and III is sufficientOption B
Statement I is not required to get answer
from statement III,
Speed of train = 400/20 = 20 m/sec
speed( in km) = 20 * 18/5 = 72 km/hr
from statement II,
time = 252/72 = 3.5 hr
statement II and III required to get answer. - What is the length of a running train A crossing another running train B ?
I. A and B two train take 18secs to cross each other, while running opposite direction.
II. The length of train B is 180mOnly I and II is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I sufficientOption D
Length of train A = l meters
from I, time taken by train to cross each other = 18secs
let speed of train A and B = x and y respectively
relative speed of A and B = (x + y) m/s
from II, length of train B = 180 meters
180 + l/x + y = 18
thus, we can not calculate answer by using these two statements. - What will be respective ratio of saving of A and B.
I. Income of A is 4% less than that of C and also expenditure of A is 12.5% less than that of C. B spend 3/5 th of his income.
II. C save rs. 7000 and A save rs.7400. Income of B is rs.1000 more than that of C.Only I is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I and II is sufficientOption E
Let income of C = 25x
income of A = 25x * 96/100 = 24x
let expenditure of A = 7y
expenditure of C = 8y
B spend 3/5 th of his his income
from II
saving of C = 7000
saving of A = 7400
Income of B is 1000 that of C
from I and II,
expenditure of A = 24x – 7y = 7400
expenditure of C = 25x – 8y = 7000
by solving two equations,
x = 600 and y = 1000
income of B = 25 * 600 + 1000 = 16000
saving B = 16000 * 2/5 = 6400
Ratio = 7400 : 6400 = 37 : 32
statement I and II is required - What is the CI on a sum at the end of 3 years ?
I. CI at the end of two years is rs.110
II. Difference between CI and SI at the end of two year is rs.100 and rate of percent is 10%.Only I is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I and II is sufficientOption B
From I,
Sum can not be find out as rate is not given
From II,
Difference PR^2/100^2
100 = P *100/10000
P = 10000
only statement II is sufficient. - I. x^2v- 41x + 348 = 0
II. y^2 – 20y + 99 = 0
X < YX > YX ≥ YX ≤ YX = Y or no relation.Option B
I. x^2 – 29x – 12x + 99 = 0
x = 29, 12
II. y^2 – 11y – 9y + 99 = 0
y = 11, 9 - I. 2x^2 – 2x _ 24 = 0
II. 3y^2 – 8y + 4 = 0
X < YX > YX ≥ YX ≤ YX = Y or no relation.Option E
I. 2x^2 – 8x + 6x – 24 = 0
x = 8, – 6
x = 4, -3
II. 3y^2 – 6y – 2y + 4 = 0
3y = 6, 2
y = 2, .67 - I. 5x^2 – 28x + 15 = 0
II. 3y^2 – 29 y + 68 = 0
X < YX > YX ≤ YX ≥ YX = Y or no relation.Option E
I. 5x^2 – 25x – 3x + 15 = 0
5x = 25, 3
x = 5, .6
II. 3y^2 – 17y – 12y + 68 = 0
y3y = 17, 12
y = 5.66, 4 - I. x^3 = 4913
II. y^2 = 225X < YX > YX ≤ YX ≥ YX = Y or no relation.Option B
I. x^3 = 4913
x = 17
II. y^2 = 225
y = 15, -15 - I. 2x^2 – 20x + 48 = 0
II. y^2 – 15y + 56 = 0X < YX > YX ≤ YX ≥ YX = Y or no relation.Option A
I. 2x^2 – 12x – 8x + 48 = 0
2x = 12, 8
x = 6, 4
II. y^2 – 8y – 7y + 56 = 0
y = 8, 7
35
Mixed Quantitative Aptitude Questions Set 224
- What is the monthly income of Jitu ?
I. Jitu spends 85% of his income on various expenses and remaining amount he saved.
II. Monthly saving of Jitu are rs.7500.
III. Out of total money spent by Jitu in a month, one-fifth is spent on rent and remaining amount of rs.34000 on other items.Only I and II sufficientOnly II and III sufficientOnly I and II sufficientNeither I nor II and III is sufficientAny of the two statements is sufficientOption E
Let income of Jitu = rs.x
from I and II,
15% of x = 7500
x = 7500 * 100/15 = 50000
From I and III,
x * 85/100 * 4/5 = 34000
x = 50000
from I and III
4/5 th of expenditure = 34000
expenditure = 42500
income = 42500 + 7500 = 50000
thus, answer can be find out by any of two given statement - How much time will require the train to reach from point X to point Y ?
I. The train will pass the other train of equal length of 400m running opposite in direction in 16 secs
II. Distance between point X and Y is 252 km.
III. The 400m long train crosses a signal pole in 20sec.Only I and II is sufficientOnly II and III is sufficientNeither of any statement is sufficientAll statements are sufficientOnly I and III is sufficientOption B
Statement I is not required to get answer
from statement III,
Speed of train = 400/20 = 20 m/sec
speed( in km) = 20 * 18/5 = 72 km/hr
from statement II,
time = 252/72 = 3.5 hr
statement II and III required to get answer. - What is the length of a running train A crossing another running train B ?
I. A and B two train take 18secs to cross each other, while running opposite direction.
II. The length of train B is 180mOnly I and II is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I sufficientOption D
Length of train A = l meters
from I, time taken by train to cross each other = 18secs
let speed of train A and B = x and y respectively
relative speed of A and B = (x + y) m/s
from II, length of train B = 180 meters
180 + l/x + y = 18
thus, we can not calculate answer by using these two statements. - What will be respective ratio of saving of A and B.
I. Income of A is 4% less than that of C and also expenditure of A is 12.5% less than that of C. B spend 3/5 th of his income.
II. C save rs. 7000 and A save rs.7400. Income of B is rs.1000 more than that of C.Only I is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I and II is sufficientOption E
Let income of C = 25x
income of A = 25x * 96/100 = 24x
let expenditure of A = 7y
expenditure of C = 8y
B spend 3/5 th of his his income
from II
saving of C = 7000
saving of A = 7400
Income of B is 1000 that of C
from I and II,
expenditure of A = 24x – 7y = 7400
expenditure of C = 25x – 8y = 7000
by solving two equations,
x = 600 and y = 1000
income of B = 25 * 600 + 1000 = 16000
saving B = 16000 * 2/5 = 6400
Ratio = 7400 : 6400 = 37 : 32
statement I and II is required - What is the CI on a sum at the end of 3 years ?
I. CI at the end of two years is rs.110
II. Difference between CI and SI at the end of two year is rs.100 and rate of percent is 10%.Only I is sufficientOnly II is sufficientEither I or II statementNeither I nor II is sufficientOnly I and II is sufficientOption B
From I,
Sum can not be find out as rate is not given
From II,
Difference PR^2/100^2
100 = P *100/10000
P = 10000
only statement II is sufficient. - I. x^2v- 41x + 348 = 0
II. y^2 – 20y + 99 = 0
X < YX > YX ≥ YX ≤ YX = Y or no relation.Option B
I. x^2 – 29x – 12x + 99 = 0
x = 29, 12
II. y^2 – 11y – 9y + 99 = 0
y = 11, 9 - I. 2x^2 – 2x _ 24 = 0
II. 3y^2 – 8y + 4 = 0
X < YX > YX ≥ YX ≤ YX = Y or no relation.Option E
I. 2x^2 – 8x + 6x – 24 = 0
x = 8, – 6
x = 4, -3
II. 3y^2 – 6y – 2y + 4 = 0
3y = 6, 2
y = 2, .67 - I. 5x^2 – 28x + 15 = 0
II. 3y^2 – 29 y + 68 = 0
X < YX > YX ≤ YX ≥ YX = Y or no relation.Option E
I. 5x^2 – 25x – 3x + 15 = 0
5x = 25, 3
x = 5, .6
II. 3y^2 – 17y – 12y + 68 = 0
y3y = 17, 12
y = 5.66, 4 - I. x^3 = 4913
II. y^2 = 225X < YX > YX ≤ YX ≥ YX = Y or no relation.Option B
I. x^3 = 4913
x = 17
II. y^2 = 225
y = 15, -15 - I. 2x^2 – 20x + 48 = 0
II. y^2 – 15y + 56 = 0X < YX > YX ≤ YX ≥ YX = Y or no relation.Option A
I. 2x^2 – 12x – 8x + 48 = 0
2x = 12, 8
x = 6, 4
II. y^2 – 8y – 7y + 56 = 0
y = 8, 7
36
Mixed Quantitative Aptitude Questions Set 223
- Train A leaves kolkata at 8am and is travelling at a speed of 70 km/hr, 4 hours later another train B leaves kolkata and is travelling in same direction as train A in how many time (in minutes) train B will be 25 km ahead train A, if speed of train B is 100 km/hr ?
475 minutes610 minutes340 minutes620 minutes368 minutesOption B
Distance covered by train A in 4 hours = 70 * 4 = 280 km
total distance should be covered by train B from kolkata for ahead 25 km to train A
required time = 280 + 25/100-70 = 305/30 * 60 = 610 minutes - In a box there are 3 red balls, 7 white balls and 5 orange balls. If one bottle is drawn at random from the cartoon what is the probability that it is either red balls or white balls ?
2/78/93/45/72/3Option E
probability = (3C1) + (7C1)/15C1 = (3 + 7)/15 = 2/3 - Two persons A and B alone can do a piece of work in 10 days and 12 days respectively. A and B together worked for 4 days and remaining worked by C alone. If efficiency of C is 20% less than the efficiency of B then find in how many days total work will be completed ?
5 days8 days7 days12 days6 daysOption B
LCM of 10 and 12 = 60
efficiency of A = 60/10 = 6
efficiency of B = 60/12 = 5
work completed by A and B together in 4 days = (6 + 5)* 4 = 44 work
remaining work = 60 – 44 = 16 work
efficiency of C = 5 * 80/100 = 4
time required to complete the work = 16/4 = 4 work
total time to complete the work = 4 + 4 = 8 days - a and B invested rs.2500 and rs.3100 in a business respectively. After 6 months A left the business and C joined with a capital of rs.2200. At the end of 1.5 years the profit received by A and B together is how much percent more or less than that by C ?
125 3/8%140 10/11%48 3/5%152 3/7%215 3/8%Option B
Profit sharing ratio of A , B and C = (2500 * 1.5) : (3100 * .5) : (2200 * 1) = 75 : 31 : 44
more % = (75 + 31) – 44/44 * 100 = 140 10/11% - Sudha is travelling from point A to B which is 560 km apart with a certain speed. While returning he covers half the distance with 30% less speed than the usual speed and cover the remaining distance with a speed of 140 km/hr. If time taken in both cases is equal, then find the speed of Sudha while going from point A to B ?
75 km/hr80 km/hr72 km/hr84 km/hr108 km/hrOption B
Let speed of Sudha while travelling from point A to point B = 10x km/hr
time taken by Sudha while travelling from A to B = 560/10x
time taken by Sudha while returning = 280/7x + 280/140
560/10x = 280/7x + 2
56/x – 40/x = 2
x = 8
speed of Sudha = 10 * 8 = 80 km/hr - Directions : What will come in place of questions (?) marks in the following questions below ?
(15)^2 – (18)^2 + 312 = ? + 47319120184133166Option E
225 – 324 + 312 = ? + 47
– 99 + 312 = ? + 47
? = 166 - ∛1331 + 38% of 1200 – ? = 98.20
421.50213.40368.80254.20281.20Option C
11 + 456 – ? = 98.20
? = 368.80 - 1/14 + 2/7 – 1/42 = ?
2/71/34/53/54/7Option B
(3 + 12 – 1) /42 = ?
? = 1/3 - 42.30 – (11)^2 + 520 – ? = 218.40
240.80312.90422.90222.90128.46Option D
562.30 – 121 – ? = 218.40
? = 222.90 - 3/4 of 420 + 320 – 4/5 of 215 = ? + 85
420422540325378Option E
315 + 320 – 172 = ? + 85
? = 378
37
Mixed Quantitative Aptitude Questions Set 222
- While we add 4 to the numerator of the fraction and increases denominator by 50% then both become equal. When the numerator is increased by 5 and denominator is doubled then it becomes equal to the original fraction. What will be two times of that fraction ?
2/55/32/74/54/3Option B
Let the numerator and denominator of a fraction be x and y respectively.
ATQ, x + 4 = 3y/2
x + 5/2y = x/y
by solving two equations,
x = 5, y = 6
original fraction = 5/6
required fraction = 5/6 * 2 = 5/3 - Two dices are rolled together, then find probability of getting a number of one dice greater than the number on other dice ?
2/37/65/62/54/7Option C
total number of cases = 6 * 6 = 36
total cases of getting same number = (1,1), (2,2), 3,3), (4,4), (5,5), (6,6) = 6
probability = 1 – 6/36 = 5/6 - P, Q, R are three inlet pipes. Time taken by P and Q together to fill half of the tank is same as time taken by pipe R alone to fill one-sixth of the tank. If P, Q, R together can fill the tank in 9 hours, then find time taken by pipe R alone to fill the tank ?
34 hours42 hours24 hours36 yours40 yoursOption D
ATQ, 2(P+Q) = 6R
P + Q = 3R
P + Q + R = 1/9
4R = 1/9
R = 36 hours - A man cuts a square field of maximum possible area from his circular field. Find the area of the remaining circular field, if the cost of grass cutting of the square field at rs. 4 per m^2 is rs.882 ?
154 m^2126 m^2200 m^2348 m^2180 m^2Option B
Let side of square be = a meters
radius of circle = r meters
area of the square field = 220.5 m^2
diagonal of the square field = 21 m
radius of the circular field = 10.5 m
area of the circular field = 346.5 m^2
area of the remaining circular field = 126 m^2 - Rohit invested rs.1600 on CI for two years at the rate of R% p.a and gets amount of rs.2304. If man invested same sum on SI for same period of time at the rate of ( R – 8)%, then find interest he will get ?
450384420640260Option B
ATQ,
2304 = 1600 ( 1 + R/100)^2
48/40 = ( 1 + R/100)
R = 20%
New rate = (20 – 8) = 12%
required interest = 1600 * 12 * 2/100 = 384 - directions : What will be come in place of questions marks (?) in the following questions given below ?
428, 434, 446, 466, 496 ?620538580650940Option B
The series is, +(2 * 3), +(3 * 4), +(4 * 5), +(5 * 6), +(6 * 7) - 187, 193, 205, ?, 277, 373
198229240350270Option B
The series is (+6), (+12), (+24), (+48), (+96) - 144, 72, 108, 270, ?, 4252.5
320620825945480Option D
The series is, (* .5), (* 1.5), (* 2.5), (* 3.5), (* 4.5) - 81, ? 76, 92, 67, 103
7385657684Option B
The series is, (+ 2^2), (- 3^2), (+ 4^2), (- 5^2), (+ 6^2) - 11, 13, 22, ?, 115, 241
4856755082Option D
the series is, +(1^3 + 1), +(2^3 + 1), +(3^3 + 1), +(4^3 + 1), + (5^3 + 1)
38
Mixed Quantitative Aptitude Questions Set 221
- The number of boys in a class are x and the number of girls are 4 less than the number of boys. The sum of weight of boys is 630 and the average weight of boys is 45 kg. If 2 students are selected for a exam then what will be the probability that the number of boys the numbers of girls are equal ?
4/935/6982/26536/1291/5Option B
Total number of boys = x
number of girls = x – 4
the number of boys = 630/45 = 14
the number of girls = 14 – 4 = 10
probability = 14C1 * 10C1 / 24C2
= 14 * 10 * 2/24 * 23 = 35/69 - Difference between CI received in first 1.5 years at 20% per annum compounded annually and CI received in last 1.5 years at same rate of interest in compounded half yearly on the same sum is rs.495, then find the sum ?
3200048000300005200045000Option E
Let sum = 100x
total rate of in 1st 1.5 years = 20 + 10 + 20 * 10 /100 = 32%
CI received = 100x * 32/100 = 32x
CI received in last 1.5 years = 100x * 1.1 * 1.1 * 1.1 – 100x = 33.1x
difference = 33.1x – 32x = 495
1.1x = 495
x = 450
sum = 100x = 100* 450 = 45000 - X and Z alone can do a piece of work in 25 days and 30 days respectively, while Y takes as half time as X and Z take together. If they start working alternatively starting by Y, followed X and Z respectively, then find in how many days work will be completed ?
5 8/17 days12 9/11 days8 2/5 days6 3/5 days26 3/8 daysOption B
LCM of 25 and 30 = 150
efficiency of X = 150/25 = 6
efficiency of Z = 150/30 = 5
efficiency of Y = 22
when all three works alternatively
3 days work = 22 + 6 + 5 == 33 work
in total 12 days = 12/3 * 33 = 132 work
remaining work = 150 – 132 = 18
remaining work completed by Y = 18/22 = 9/11 day
total days = 12 9/11 days - A boat takes total 10 hours to cover the distance of 84 km in upstream and 84 km in downstream. If the speed of boat is increased by 12km/hr, then the new upstream speed is doubled of its usual speed. Find the time taken by boat to cover 140 km in downstream.
5826.52.5Option A
Let speed of boat = x km/hr
speed of stream = y km/hr
downstream speed = x + y
upstream speed = x – y
new speed of boat = x + 12
upstream speed = x + 12 – y
2 (x – y ) = x + 12 – y
x – y = 12
upstream speed = 12
time taken by boat to cover 84 km in upstream 84/12 = 7
time taken by boat in downstream = 10 – 7 = 3
downstream speed = 84/3 = 28 km
time taken by boat to cover 140 km in downstream = 140/28 = 5 hours - A and B started a partnership business with investment (x + 500) and (x – 1000) respectively. After 6 months a withdrew 40% of his amount. If profit received by A at the end of the year is 2800 out of the total profit rs.4800, then what is the value of ‘x’ ?
40002000150030005600Option D
Investment of A = (x + 500)* 6 + ( x + 500)* .6 * 6 = 6(1.6x + 800)
investment of B = (x – 1000) * 12
profit of A = 2800
profit B = 4800 – 2800 = 2000
6( 1.6x + 800)/(x – 1000)12 = 2800/2000
8x + 4000 = 14x – 14000
x = 3000 - I. 2x^2 – 13x + 15 = 0
II. y^2 – 6y + 8 = 0
X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. 2x^2 – 10x – 3x + 15 = 0
2x = 10, 3
x = 5 , 1.5
II. y^2 – 4y – 2y + 8 = 0
y = 4, 2 - I. x^2 – 27x + 92 = 0
II. y^2 – 17y + 60 = 0
X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 – 23x – 4x + 92 = 0
x = 23, 4
II. y^2 – 12y – 5y + 60 = 0
y = 12 , 5 - I. x^2 = 196
II. y^3 = 4096X > YX < YX ≤ YX ≥ YX = Y or no relation.Option B
I. x^2 = 196
x = 14, -14
II. y^3 = 4096
y = 16 - I. 5x^2 – 7x + 2 = 0
II. y^2 + 12y + 32 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option A
I. 5x^2 – 5x – 2x + 2 = 0
5x = 5, 2
x = 1, .4
II. y^2 + 8y + 4y + 32 = 0
y = -8, -4 - I. 3x^2 – 19x + 20 = 0
II. 4y^2 – 6y + 2 = 0
X > YX < YX ≤ YX ≥ YX = Y or no relation.Option A
I. 3x^2 – 15x – 4x + 20 = 0
3x = 15, 4
x = 5, 1.33
II. 4y^2 – 4y – 2y + 2 = 0
4y = 4, 2
y = 1. .5
39
Mixed Quantitative Aptitude Questions Set 220
- A shopkeeper X sold an article for rs.850 at a profit of 25%. Another shopkeeper Y sold the another article and earned 30% more profit than the profit earned by X. If the selling price of article Y is three-fifth of selling price of article X, then find the profit percent of article Y ?
64 2/17%76 8/17%52 3/34%52 3/8%78%Option B
SP of article X = 850
CP of article X = 850 * 100/125 = 680
profit = 170
profit of article Y = 170*130/100 = 221
SP of article Y = 850 * 3/5 = 510
CP = 510 – 221 = 289
profit percent = 221/289* 100 = 76 8/17% - Mixture A contains milk and water in the ratio of 3 : 2 respectively, while mixture B contains water and milk in the ratio of 4 : 3 respectively. If the quantity of water in mixture B is twice the quantity of water in mixture A, then find the quantity of milk in mixture A is what percent quantity of water in mixture B ?
68%60%82%75%56%Option D
Quantity of milk and water in mixture A = 3x and 2x
according to questions,
quantity of water in mixture B = 2*2x = 4x
quantity of milk in mixture B = 4x/4 *3 = 3x
required percentage = 3x/4x*100 = 75% - 340 liters of mixture of milk and water is contained in a container having milk and water mixed in the ratio of 3 : 1 respectively. 76 liters of this mixture is taken out from the container and replaced with (x + 7) liters of milk so that the ratio of water to milk is 6 : 11. What is the value of ‘x’ ?
4248383552Option D
Quantity of milk in the container = 340 * 3/4 = 255
quantity of water in the container = 340*1/4 = 85
76 liters of mixture is taken out and (x + 7) liter of water is added.
(255 – 57) / 85 – 19 + (x + 7) = 11/6
198/(73 + x) = 11/6
11x = 385
x = 35 - A can do a piece of work in 30days while B and C together can complete the work in 20 days and A and C together can complete the work in 24 days. If B is worked in two-fifth of his efficiency, then in how many days A and B together complete half of the work ?
8 days6 days8 1/3 days5 days10 daysOption E
LCM of 30 , 20 and 24 = 120
efficiency of A = 120/30 = 4
efficiency of B and C = 120/20 = 6
efficiency of A and C together = 120/24 = 5
efficiency of C = 5- 4 = 1
efficiency of B 6- 1 = 5
two-fifth of efficiency B = 5 * 2/5 = 2
time required to complete half of the work = 60/2 + 4 = 10 days - Rohan and Sivan started a business together with initial investments of rs. 1500 and rs.1800 respectively. If after 2.5 years profit share of Rohan and Sivan are rs(x + 80) and (x + 120) respectively, then find the difference between profit of Rohan and Sivan ?
180120320130340Option B
Profit sharing ratio of Rohan and Sivan = (1500 * 2.5) : (1800 * 2.5) = 5 : 6
x + 80/x + 120 = 5/6
6x + 480 = 5x + 600
x = 120 - Directions : In each of these questions given below two equations. You have to solve both the equations and give answer.
I. x^2 – 7√3 + 36 = 0
II. y^2 – 6√2 + 16 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 – 4√3 – 3√3 + 36 = 0
x = 4√3 , 3√3
II. y^2 – 4√2 – 2√2 + 16 = 0
y = 4√2, 2√2 - I. x^2 + √2x – 12 = 0
II. y^2 – 8√3 + 48 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option B
I. x^2 + 3√2 – 2√2 – 12 = 0
x = -3√2, 2√2
II. y^2 – 4√3 – 4√3 + 48 = 0
y = 4√3, 4√3 - I. x^2 – 36 = 0
II. y^2 – 15y + 36 = 0
X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 = 36
x = 6, -6
II. y^2 – 12y – 3y + 36 = 0
y = 12, 3 - I. y^2 = 144
II. 2x^2 – 12x + 16 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. y^2 = 144
y = 12, -12
II. 2x^2 – 8x – 4x + 16 = 0
2x = 8, 4
x = 4, 2 - I. x^2 – 2x – 195 = 0
II. y^2 – 24y + 128 = 0X > YX < YX ≤ YX ≥ YX = Y or no relation.Option E
I. x^2 – 15x + 13x – 195 = 0
x = 15, -13
II. y^2 – 16y – 8y + 128 = 0
y = 16, 8
40
Mixed Quantitative Aptitude Questions Set 219
- A man deposited a total amount of rs. 36000 partially in scheme A and scheme B. Scheme A offers simple interest at the rate of 14% p.a while scheme B offers compound interest at the rate of 20% p.a compounded annually. If the interest earned from scheme A after 2 years is rs.2160 less than the interest earned from scheme B after 2 years, then what is the amount deposited in scheme B ?
1500017000230001400017500Option B
Let amount deposited in scheme B = rs. x
amount deposited in scheme A = rs.(36000 – x)
Rate of compound interest after 2 years = 20 + 20 + 20 * 20/100 = 44%
x * 44/100 – (36000 – x) * 14/100 * 2 = 2160
(44x – 108000 + 28x)/100 = 2160
72x = 1224000
x = 17000
amount deposited in scheme B is rs.17000 - The income of A and B are in the ratio 4 : 5 respectively. If the expenditure of A and B are rs.14000 and rs.18000 and ratio of saving of A and B is 6 : 7, then what is the saving of B ?
80009200700068008200Option C
Let income of A and B = 4x and 5x respectively
4x – 14000/5x – 18000 = 6/7
28x – 98000 = 30x – 108000
x = 5000
income of B = 5 * 5000 = 25000
saving of B = 25000 – 18000 = 7000 - A takes 5 days less than B to complete a work alone. A and B together can complete the work in 13 7/11 days. Find the time taken by B to complete the whole work ?
25 days30 days45 days43 days40daysOption B
Let B alone can complete the whole work = x days
A alone can complete the whole work = (x – 5) days
1/x – 5 + 1/x = 11/150
2x – 5/x^2 – 5x = 11/150
11x^2 – 55x = 300x – 750
11x^2 – 355x + 750 = 0
11x^2 – 330x – 25x + 750 = 0
x = 30
B alone can complete the whole work in 30 days - Three containers having capacity in the ratio of 4 : 5 : 3 contain mixture of milk and water in the ratio of 2 : 3, 4 : 1 and 3 : 1 respectively. If all three containers poured in a big container, then find the ratio of water to milk in final mixture ?
28 : 13785 : 15283 : 157134 : 495 : 2Option C
Let total mixture in three container are 400, 500 and 300 respectively
total quantity of milk in big container = 400 * 2/5 + 500 * 4/5 + 300 * 3/4 = 785
total quantity of water in big container = 400 * 3/5 + 500 * 1/5 + 300 * 1/4 = 415
required ratio = 415 : 785 = 83 : 157 - B and C started a partnership business with the capital of rs.(x + 4000) and rs.(x + 2000) respectively. After one year A joined the business with capital of rs.(x + 12000) while B left the business. If at the end of three years the profit sharing ratio of A , B and C is 20 : 6 : 15, then find the difference between amount invested by A and B in the business ?
150001300014000800012000Option D
A : B : C = (x + 12000) * 2 : (x + 4000) * 1 : (x + 2000) * 3
= 2x + 24000 : x + 4000 : 3x + 6000
2x + 24000/x + 4000 = 20/6
20x + 80000 = 12x + 144000
8x = 64000
x = 8000
difference = (8000 + 12000) – (8000 + 4000) = 8000 - Directions : In these questions two equations is given, solve the equations and answer the questions given below.
I. x^2 – 42x + 392 = 0
II. y^2 – 27y + 180 = 0X < YX > YX ≤ YX ≥ YX = Y or no relationOption E
I. x^2 – 28x – 14x + 392 = 0
x = 28 , 14
II. y^2 – 15y – 12y + 180 = 0
y = 15, 12 - I. x^2 – 8x – 65 = 0
II. 2y^2 – 27y + 91 = 0
X < YX > YX ≤ YX ≥ YX = Y or no relationOption E
I. x^2 – 13x + 5x – 65 = 0
x = 13, -5
II. 2y^2 – 14y – 13y + 91 = 0
2y = 14, 13
y = 7, 6.5 - I. x^3 = 216
II. 5y^2 + 2y – 185 = 0X < YX > YX ≤ YX ≥ YX = Y or no relationOption B
I. x^3 = 216
x = 6, 6
II. 5y^2 + 15y – 13y – 37 = 0
5y = – 15, 13
y = -3 , 2.6 - I. x^2 + 17x + 60 = 0
II. y^2 – 2y – 15 = 0X < YX > YX ≤ YX ≥ YX = Y or no relationOption A
I. x^2 + 12x + 5x + 60 = 0
x = -12, -5
II. y^2 – 5y + 3y – 15 = 0
y = 5, -3 - I. x^2 – 15x + 36 = 0
II. y^2 – 19y + 60 = 0X < YX > YX ≤ YX ≥ YX = Y or no relationOption E
I. x^2 – 12x – 3x + 36 = 0
x = 12 , 3
II. y^2 – 15y – 4y + 60 = 0
y = 15, 4
41
Mixed Quantitative Aptitude Questions Set 218
- Ratio of number of male of company X to company Y is 8 : 5. The ratio of female to male of company X and company Y is 3 : 4 and 7 : 5 respectively. The difference between number of female of company X and company Y is 150, then find total number of male and female in company Y ?
27002200180015001200Option C
Let the number of male of company X and Y = 8a and 5a
number of male and female of company X = 4a and 3a
number of male and female of company Y = 5a and 7a
The number of male and female of company X = 8a and 6a
difference = 7a – 6a = 150
a = 150
sum of number of male and female of company Y = 5a + 7a = 12a
= 12 * 15 = 1800 - A and B entered into a partnership business with initial investments of rs.4000 and rs.5000 respectively. After 6 months A and B withdrew rs.1000 and rs.2000 respectively, while C joined with them capital of 4x. If after 14 months, C received rs.4000 as profit share out of total profit of rs.12500, then find how much amount invested by C ?
40004500480060003200Option D
Profit sharing ratio of A, B and C = (4000 * 6 + 3000 * 8) : (5000 * 6 + 3000 * 8) : 4x * 8
= 48000 : 54000 : 32x
profit of A and B = 12500 – 4000 = 8500
32x/102000 = 4000/8500
x = 1500
C invested = 4 * 1500 = 6000 - Rohit invested rs.100x in a scheme offering compound interest at the rate of 20% p.a and after two years he again invested rs.80x in the same scheme. He received rs. 1243.2 as total interest after 3 years. If he rs.120x is invested at 10% p.a simple interest for 4 years the find how much interest he received ?
1128672845862920Option B
Compound interest after 2 years = 100x * 120/100 * 120/100 – 100x = 44x
now total principal = 100x + 44x + 80x = 224x
CI received after one year = 224x * 20/100 = 44.8x
total CI after 3 years = 88.8x
88.8x = 1243.2
x = 14
If he received 120x at 10% p.a in SI for 4 years
120 * 14 * 40/100 = 672 - The ratio of milk and water in Jar A is 5 : 3 and total mixture of container A is 480 liters. Jar B contains mixture of water to milk in the ratio of 7 : 9. Total mixture of jar A and B poured into another jar C such that quantity of milk in jar C is 60% of total mixture. Find the quantity of mixture in jar B ?
440 lt480 lt380 lt240 lt320 ltOption E
Quantity of milk in jar A = 480 * 5/8 = 300
quantity of water in jar B = 480 * 3/8 = 180
let the quantity of milk and water in jar B = 9x and 7x
300 + 9x = (480 + 16x) * 60/100
1500 + 45x = 48x + 1440
3x = 60
x = 20
total mixture in jar B = (9x + 7x) * 20 = 320 liters - A man deposited rs.8000 in a bank offering compound interest of 20% p.a compound annually for first 1.5 years and after 1.5 years he offering simple interest 50% p.a for rest of the time. If at the end of 1.5 years, he withdrew rs.3560, then how much amount received by him at the end of 3 years ?
1240010500180001225015240Option D
Rate of compound interest after 1.5 years = 20 + 10 + 20 * 10/100 = 32%
total amount after 1.5 years = 8000 * 132/100 = 10560
remaining amount after withdrawal by him = 10560 – 3560 = 7000
simple interest received for rest of time = 7000 * 1.5 * 50/100 = 5250
total amount received = 7000 + 5250 = 12250 - Directions : What will come in place of questions (?) marks in the following questions given below ?
30% of 168 + √1024 + 42 = ?84.294.8124.46584Option C
50.4 + 32 + 42 = ?
? = 124.4 - (25^2) + (38^2) – 1220 + ? = 1000
151162170175320Option A
625 + 1444 – 1220 + ? = 1000
? = 1000 – 849
? = 151 - (32 * 8 + 440 + 15 * 12) * 6 = ?
43403240201552568450Option D
(256 + 440 + 180) * 6 = ?
? = 5256 - 5^2 + 387 = 180/? + 376
68457Option D
25 + 387 = 180/? + 376
412 – 376 = 180/?
? = 5 - 75 * 8 + √1156 = ?^3 + 122
4321484Option D
600 + 34 = ?^3 + 122
?^3 = 512
? = 8
42
Quantitative Aptitude: Simplification Questions Set 118
Direction: What is the approximate value in the place of questions mark (?) in the following questions ?
- 887.97÷12.06*√16.05-36=?
268260280300240Option B
888/12*4-36=?
?=296-36=260 - ?^2+56.01-24*5.99=168.01
1615132024Option A
168+144-56=?^2
?=16^2 - 45.01% of 4500÷15.05+139.88-220.01=?
6065557085Option C
2025/15+140-220=?
135+140-220=55 - (7.99)^2+(10.01)^2-(18.05)^2+(12.99)^2=?
151391228Option C
8^2+10^2-18^2+13^2=?
64+100-324+169=?
?=9 - 539.98/?=?/60.01
200160120180200Option D
?^2=540*60
?^2=540*60
?=180 - 36% of 1000+42% of 3000=?-180+1050
750650850950550Option A
360+1260+180-1050=750 - 5/11 of 1331+4/9 of 270=30% of 400+30+?
680575675550740Option B
605+120-120-30=?
?=575 - 2748+1323-2238-1235+3248=?
36463948374838462896Option D
7319-3473=3846 - 4515÷15+324-25% of 1200=?
325425320440345Option A
301+324-300=325 - 48/3*45/80*1/9+135-40=?
1181057896120Option D
48/3*45/80*1/9+135-40=?
1+135-40=96
Direction: What will come in the of questions mark(?) in the following questions.
43
Quantitative Aptitude: Ratio and Proportion Questions Set 14
- In a mixture of 80 liters, the ratio of milks and water is 3:2 . How much water must be added to this mixture so that the ratio of milk and water becomes 3:4.
2428403632Option E
Total mixture =80 liters.
milk =80*3/5 =48
water =80*2/5 =32
Let, x liters of water is added.
48/32+x =3/4
32+x =64
x =64-32 =32 liters. - In a school the students of three classes are in the ratio of 2:3:5 . If 20 students are increased in every class the ratio of changes is 4:5:7. What is the total number of students in the three classes before the class increased .
200100250300400Option B
Let students in three classes be
2x, 3x and 5x respectively.
According to the question ,
(2x+20):(3x+20):(5x+20) =4:5:7
2x+20/3x+20 =4/5
12x+80 =10x+100
2x=20
x=10
Total students =(2*10)+(3*10)+(5*10)
= 20+30+50 =100 - If 16 cows cost as much as 8 bullocks, 10 bullocks cost as much as 5 horses and 3 horses cost as much as 4 camels. If the cost of one camel is rs.3300. Find the cost of one cow is,
21002200230011001200Option D
1 camel cost=3300
4 camel cost=13200
3 horses cost=13200
1 horses cost=4400
5 horses cost=22000
10 bullocks cost=22000
1 bullocks cost=2200
8 bullocks cost =17600
16 cows cost =17600
1 cows cost =1100 - The ratio of the earning of A and B is 3:5. If the earning of a increased by one-forth and the earning of B decreased by one-forth, then find the new ratio of their earning ?
2:31:13:45:22:5Option B
Let earning of A and B be 3x and 5x.
New ratio of their earning = 3x*5/4:5x*3/4 =1:1 - A some of money is to be distributed among A,B,C,D in the proportion of 3:5:2:4 . If D gets 3000 more than C, then find total money which is distribute among all.
3000021000250002800024000Option B
Let the money is distributed among A,B,C and D be 3x,5x,2x and 4x respectively.
4x-2x =3000
2x =3000
x =1500
total amount of money distributed =3x+5x+2x+4x =14x
= 14*1500 =21000 - The ratio of the number of boys and girls in a college is 7:9. If the percentage increase in the number of boys and girls be 20% and 30% respectively. The total number of boys and girls in college before increase is 1440, then find ratio of boys and girls in the college after increased.
28:3938:4325:2835:2830:37Option A
ratio of boys and girls=7:9
total boys and girls=1440
boys=1440*7/16=630
girls=1440*9/16=810
the number of boys after increased=630*120/100=756
the number of girls after increased=810*130/100=1053
ratio of boys and girls after increased=756:1053=28:39 - Salaries of Ram and Rohit are in the ratio of 4:5. If the salary of each is increased by rs.3000, the new ratio becomes 10:11. What is initial salary of Rohit.
27003000420025003500Option D
let salaries of Ram and Rohit be 4x and 5x
(4x+3000)/(5x+3000)=10/11
44x+33000=50x+30000
6x=3000
x=500
initial salary of Rohit=5x=5*500=2500 - A contains a mixture of 56 liters of wine and water in the ratio of 3:4 . If 28 liter of mixture is taken and 8 liter of wine is added , then find the ratio of new mixture .
3:28:35:55:43:4Option D
Ratio of wine and water =3:4
wine =56*3/7 =24
water =56*4/7 =32
28 liter of mixture taken out wine = 24-(28*3/7) =24-12 =12
water=32-(24*4/7) =32-16 =16
8 liters of wined is added then ,
new ratio of wine and water =(12+8):16 =20:16 =5:4 - 48% of A is equal to 64% of B, then find the ratio of A and B ?
3:23:47:35:44:3Option E
48% of A = 64% of B
A/B=64/48=4:3 - The ratio of three numbers is 2:4:5 and sum of their squares is 1125. Find the sum of the numbers.
6045505565Option D
ratio of three numbers=2:4:5
let the numbers be 2x, 4x and 5x
sum of their squares=1125
4x^2+16x^2+25x^2=1125
45x^2=1125
x^2=25
x=5
the sum of the numbers=2x+4x+5x=11x=11*5=55
44
Quantitative Aptitude: Quadratic Equations Questions Set 78
- x^2+14x+24 =0
y^2+18x+65 =0X>YXX≥YX≤YX=Y or no relationOption E
I. x^2+12x+2x+24 =0
x= -12, -2
II. x^2+13x+5x+65 =0
x= -13, -5 - I. 2x^2+23x++65 =0
II. 3x^2+25x+50=0X>YXX≥YX≤YX=Y or no relationOption D
I. 2x^2+13x+10x+65=0
2x=-13, -10
x=-6.5, -5
II. 3x^2+15x+10x+50 =0
3x= -15,-10
x=-5, -3.33 - I. x^2-18x+72=0
II. y^2-8y+15 =0
X>YXX≥YX≤YX=Y or no relationOption A
I. x^2-12x-6x+72=0
x =12, 6
II. y^2-5y-3y+15 =0
y=5, 3 - I. x^3= 729
II. y =√81X>YXX≥YX≤YX=Y or no relationOption E
I. x^3=729
x=9
II. y=9 - I. x^2-11x+18 =0
II. y^2-23y+132 =0X>YXX≥YX≤YX=Y or no relationOption B
I. x^2-9x-2x+18 =0
x=9, 2
II. y^2-12y-11y+132 =0
y^2 =12, 11 - I. 4x^2-12x+5 =0
II. 2y^2+3y-5=0X>YXX≥YX≤YX=Y or no relationOption E
I. 4x^2-10x-2x+5 =0
4x=10, 2
x= 2.5, .5
II. 2y^2+5y-2y-5 =0
2y= -5, 2
y= -2.5, 1 - I. x^2-3x+28 =0
II. y^2+3y-18=0X>YXX≥YX≤YX=Y or no relationOption E
I. x^2-7x+4x+28=0
x=7, -4
II. y^2+6y-3y-18=0
y=-6, 3 - I. x^4=256
II. y^3=64X>YXX≥YX≤YX=Y or no relationOption D
I. x^4=256
x=4, -4
II. y^3=64
y=4, 4 - I. x^2-35x+250=0
Ii. y^2-14y+40=0X>YXX≥YX≤YX=Y or no relationOption C
I. x^2-25x-10x+250=0
x=25,10
II. y^2-10y-4y+40=0
y=10,4 - I. x+5=√100
II. y+8=√144X>YXX≥YX≤YX=Y or no relationOption A
I. x+5=√100
x+5=10
x=5
II. y+8=√144
y+8=12
y=4
45
Quantitative Aptitude: Number Series Set 157
- 32, 80, 200, 500, 1250 ?
31254125250037505125Option A
The series is (32*2.5), (80*2.5), (200*2.5)….. - 12, 29, 63, 131, 267, ?
541538429539342Option D
The series is (*2+5), (*2+5)… - 48, 51, 56, 63, ?, 87
7274757876Option B
The series (+3), (+5), (+7), (+11), (+13) the addition of prime numbers. - 1248, 1184, 1135, 1099, 1074, ?
115853810581220625Option C
The series (-8^2), (-7^2), (-6^2)… - 6420, 6435, 6465, 6510, ?, 6645
64206500653065706424Option D
The series is (+15), (+30), (+45)… - 8, 8, 12, 28, 88, 932
2888932128Option B
The series is (*.5+4), (*1+4), (*2+4), (*4+4), (*8+4) - 320, 330, 310, 340, 300, 360
300360340320310Option B
The series is (+10), (-20), (+30), (-40), (+50) - 32, 33, 41, 68, 114, 257
257684111433Option D
The series is (+1^3), (+2^3), (+3^3), (+4^3), (+5^3 ) - 18, 36, 108, 432, 2160, 12360
12360216043210836Option A
The series is (*2), (*3), (*4)… - 45, 49, 41, 45, 37, 42
4549414237Option D
The series is (+4), (-8), (+4), (-8), (+4)
46
Quantitative Aptitude: Number Series Set 156
- 960, 839, 758, 709, 684, ?
685550485675745Option D
the series is, (-11^2), (-9^2), (-7^2)… - 340, 356, 382, 418, 464, ?
520480540516496Option A
the series is, +16, +26, +36, +46, +56 - 15, 41, 78, 128, 193, ?
278275385345264Option B
the series is, +(5^2+1), +(6^2+1), +(7^2+1)… - 335, 351, 383, 431, ?, 575
487535530485495Option E
the series is, +16, +32, +48, +64, +80 - 13, 15, 21, 33, 53, ?
8396958580Option A
the series is, +(1*2), +(2*3), +(3*4), +(4*5), +(5*6) - 8, 18, 57, 232, 1165, 6994
11652325769948Option D
the series is, (*2+2), (*3+3), (*4+4)… - 14, 20, 32, 44, 58, 74
1420327444Option B
the series is, +8, +10, +12, +14, +16 - 244, 202, 172, 152, 140, 132
132140244172152Option A
the series is, -(6^2+6), -(5^2+5), -(4^2+4)… - 35, 44, 28, 53, 17, 65
3565175328Option B
the series is, +3^2, -4^2, +5^2, -6^2, +7^2 - 36, 23, 28, 47, 99, 252
99472825236Option D
the series is, (*.5+5), (*1+5), (*1.5+5), (*2+5), (*2.5+5)
47
Quantitative Aptitude: Simplification Questions Set 117
- Direction: What will come in place of question(?) marks in the following questions ?
13540+12981+1519-? =250004260314033403040none of theseOption D
13540+12981+1519-25000 =3040 - (1696÷4-?)10=1200
404304340420520Option B
(424-x)10 =1200
4240-10x =1200
x =304 - 19*12*8+94 =?
19182018220019001920Option A
1824+94=1918 - 120% of 55+240% of 25+? =140
1614202224Option B
66+60+? =140
?=14 - (196/27*4)*(8/20)*(180/9)*(81/7)= ?
178210180168none of theseOption D
7*8*3 =168 - Direction: What will come in place of ‘x’ in the following questions given below ?
20% of 25% of 40% of 1200 =x+82216121815Option B
1/5*1/4*2/5*1200 =x+8
x= 24-8 =16 - 52^2+62^2+75^2-85^2 =x+48
5000600052004200none of theseOption A
2704+3844+5625-7225-48 =x
12273-7225-48 =x
x =5000 - √3025+√1600-81+x=79
5564606570Option D
55+40-81+x =79
x= 65 - 520/13+980-1020/17+20% of 55 =x+88
883880920780783Option A
40+980-60+11 =x+88
x= 883 - 168÷21*8+218+x =525
345445355245280Option D
64+218+x =527
x= 527-282
x= 245
48
Quantitative Aptitude: Ratio and Proportion Questions Set 13
- The ratio of amount of A and B is 4 : 3 and the ratio of amount of B and C is 4 : 5 . If the total number of amount A , B and C have rs. 3870, then find the how much amount B have ?
120023401080880960Option C
Ratio of amount of A and B = 4 : 3
ratio of amount of B and C = 4 : 5
By multiplying ‘4’ in ratio of A and B
A : B = (4 : 3) 4 = 16 : 12
By multiplying ‘3’ in ratio of B and C
B : C = (4 : 5) 3 = 12 : 15
A : B : C = 16 : 12 : 15
let amount of A , B and C have = 16x , 12x and 15x
total = 43x
43x = 3870
x = 90
12x = 1080
B have = 1080 - Rabin has three types of coins i.e 10 paisa , 20 paisa and 50 paisa and total value of this coins is rs. 78. The number of coins is in the ratio of 6 : 4 : 5. Find the number 10 paisa coins.
180300120140420Option C
Let the number coins of 10 paisa , 20 paisa and 50 paisa is 6x, 4x and 5x respectively.
(10 * 6x) + (20 * 4x) + (50 * 5x) = rs. 78
60x + 80x + 250x = 78
390x = 7800
x = 20
The number 10 paisa coins = 6 * 20 = 120 - A sum of amount of rs. 3500 is divided between three friends. The ratio of amount given to P and Q is 2 : 3 and Q and R is 3 : 5. What is difference the amount given to P and R ?
124094048010501280Option D
Let the amount given to P and Q = 2x and 3x
Q and R = 3x and 5x
total amount = 3500
2x + 3x + 5x = 3500
10x = 3500
x = 350
difference = 5x – 2x = 3x = 3 * 350 = 1050 - Rohit gave half of his monthly salary to his parents and one-third of remaining salary to his wife and remaining his salary gave to his son and daughter in the ratio of 13 : 12. If his monthly salary is rs.45000, then find how much amount he gave to his son ?
45003450630052007800Option E
Rohit gave to his parents = 45000/2 = 22500
remaining salary = 45000 – 22500 = 22500
he gave to his wife = 22500 * 3 = 7500
remaining salary = 22500 – 7500 = 15000
he gave to his son = 15000 * 13/25 = 7800 - Two numbers are in the ratio of 4 : 3. When we added 60 in each number the ratio becomes 30 : 23. Find the sum of both initial numbers.
15202000147038002540Option C
Let two numbers is 4x and 3x
When we added 60
4x + 60 / 3x + 60 = 30/23
92x + 1380 = 90x + 1800
2x = 420
x = 210
total sum = 4x + 3x = 7x = 7 * 210 = 1470 - The ratio of income of Rahul and Raju in the ratio of 6 : 5 and they saved rs. 1500 each, Their expenditure ratio 9 : 7 , then find what is the sum of their incomes ?
1400018000350002000011000Option E
Let income of Rahul and Raju = 6x and 5x
they saved = 1500 each
6x – 1500 / 5x – 1500 = 9/7
42x – 10500 = 45x – 13500
3x = 3000
x = 1000
sum = 6x + 5x = 11 * 1000 = 11000 - There are total of 300 employees in a company. The ratio of male employees to female employees are 8 : 7. How many female employees have to be recruited so that the ratio
becomes male and female is equal ?4080256220Option E
Number of male = 300 * 8/15 = 160
number of female = 300 * 7/15 = 140
let ‘x’ number of female we added
160 = 140 + x
x = 20 - If the numerator is increased by 20 % and the denominator is decreased by 20% so that fraction becomes 2 : 3. What is the original fraction ?
2/55/94/92/34/11Option C
Let the numerator and denominator be x and y respectively
(x * 120/100) / (y * 80/100) = 2/3
(6x/5) /(4y/5) = 2/3
6x / 4y = 2/3
18x = 8y
x/y = 8 /18 = 4/9 - Total number of workers worked in a company is 50 and the ratio of male workers to female workers is 3 : 2. The ratio of amount of wages received by a male and a female worker is 7 : 6. If the wages received by each female workers is rs.120, then how much total wages received by all male workers ?
38003200450042006500Option D
Total workers = 50
male workers = 50 * 3/5 = 30
female workers = 50 * 2/5 = 20
wages received by a female workers = 120
wages received by a male workers = 120/6 *7 = 140
total wages received by all male workers = 140 * 30 = 4200 - Three friends A , B and C got a total prize money is rs.2149. If B got 15% more A and C got 20% less than B, then find the how much amount of money C get ?
520644440634460Option B
Total prize money = 2149
let A got = 100x
B got = 100x * 115/100 = 115x
C got = 115x * 80/100 = 92x
total = 100x + 115x + 92x = 307x
amount of money C got = 2149/307x * 92x = 644
49
Quantitative Aptitude: Profit and Loss Set 29
- A man purchase is a bike for rs.75400 and spends rs. 2600 for his its maintenance. After some days he sells the bike at rs. 89700. What is his profit percentage ?
10%18%11%15%8%Option D
CP of bike = 75400
maintenance cost = 2600
total cost price of Bike = 75400 + 2600 = 78000
profit = 89700 – 78000 = 11700
profit percentage = 11700/78000 * 100 = 15% - Ayush made a loss of 10% on selling a cycle. If he would have made a profit of 40%. In what price he would sell so that he can get 22% profit ?
15201840248018302240Option D
Let CP of cycle = 100x
loss = 10%
SP of cycle = 100x * 90/100 = 90x
If he sold 750 more, he would have 40% profit
SP = 100x * 140/100 = 140x
90x + 750 = 140x
50x = 750
x = 15
CP = 100x = 1500
SP = 1500 * 122/100 = 1830 - Marked price of an article is 45% above its cost price and by giving 20% discount on marked price he earned rs.128 as profit. What is profit percent incurred when he sells same article rs.72 more than its selling price.
22%28%34%25%12%Option D
Let CP of article = 100x
MP of article = 100x * 145/100 = 145x
SP of article = 145x * 4/5 = 116x
profit = rs.128
116 x – 100x = 16x
16x = 128
x = 8
CP = 800
SP = 928
When he sells rs.72 more than its SP,
SP = 928 + 72 = 1000
Profit % = 1000 – 800/800 * 100 = 25% - Rohit purchased a mobile rs.4500 and sold it at 20% loss to Reema. Which amount he got from Reema, he purchased a TV and sold it at a profit of 25%. How much amount of overall profit or loss made by him in whole transactions ?
180470200350No profit no lossOption E
CP of mobile = 4500
he sold at 20% loss,
SP of mobile = 4500 * 4/5 = 3600
CP of TV = 3600
he sold at 25% profit,
SP = 3600 * 5/4 = 4500
there is no profit no loss - A shopkeeper marked up the price of an article 60% above the cost price. If he gives a successive discount of 15% and 10% on marked price, so that selling price of the article is rs.24480. Find the cost price.
22002000124013501430Option B
Let CP of article = 100x
MP of article = 160x
SP of article = 160x * 85/100 * 90/100 = 122.4x
122.4x = 2448
x = 2448/122.4 = 20
CP = 100x = 2000 - A man buys 40 mangoes at rs. 5 each and 60 oranges at rs.4 each. 10% of the mangoes and oranges are rotted. The man sells the remaining mangoes at rs. 7 each and oranges at rs 3 each. Find the overall gain or loss percentage ?
8% profit10% loss22% loss65/11% loss14%Option D
Total CP of 40 mangoes = 40 * 5 = 200
Total CP of 60 mangoes = 60 * 4 = 240
10% of mangoes and oranges are rotted
remaining mangoes = 40 * 90/100 = 36
and oranges = 60 * 90/100 = 54
total SP of oranges = 54 * 3 = 162
total SP = 252 + 162 = 414
loss % = 440 – 414 /440 * 100 = 65/11% - A shopkeeper sold a product at 20% discount and profit earned on that product is 16.67%. If the marked price of that product is rs.875, then what is the cost price of that product ?
820340680600485Option D
MP of the product = 875
SP of product = 875 * 4/5 = 700
profit = 16.67% = 1/6
let CP = 6x
profit = x
SP = 7x
7x = 700
x = 100
CP = 6x = 600 - A dishonest shopkeeper sold rice at cost price. The 1kg weight of rice that he uses actually weight of 780 gm. How much percentage profit does he earned on the sale of 1kg price ?
200/6%120/7%18%1100/39%204/5%Option D
Actual weight = 1kg
false weight = 780 gm
profit = 100 – 780 = 220
profit % = 220/780 * 100 = 1100/39% - Sekhar sells two products A and B have equal cost price. Product A is sold at 30% profit and product b is sold at an amount of 15% less than the selling price of product A. If the total profit is rs.162, then what is cost price of B ?
480400525340260Option B
Let CP of the product A = x
SP of product A = x * 130/100 = 13x/10
SP of product B = 13x /10 * 17/20 = 221x/200
profit of product A = 13x/10 – x = 3x /10
profit of product B = 221x/200 = 21x/200
3x/10 + 21x/200 = 162
60x + 21x / 200 = 162
x = 400 - An article is sold at a profit of 15%. If it had been sold at a profit of 22%, it would have fetched rs. 340 more. What is the cost price of article ?
25003240145020004420Option D
Let CP of the article = 100x
SP of the article = 100x * 115/100
when it sold at 22% profit
SP = 100 * 122/100 = 122x
122x – 115x = 7x
7x = 340
x = 20
CP of the product = 100x = 100 * 20 = 2000
50
Quantitative Aptitude: Number Series Set 155
- Directions : What will come in place of questions ( ? ) marks in the following number series ?
8 , 46 , 80 , 110 , 136 , ?168158208425384Option B
The series is (+ 38) , (+ 34) , (+ 30) , (+ 26) , (+ 22) - 29 , 32 , 61 , 93 , 154 , ?
285160247240320Option C
The series is (29 + 32 = 61) , (32 + 61 = 93) , (61 + 93 = 154) , (93 + 154 = 247) - 65 , 83 , 103 , 125 , ? , 175
128165143149120Option D
The series is , + (8^2 + 1) , + (9^2 + 2) , + (10^2 + 3) , + (11^2 + 4) , + (12^2 + 5) , + (13^2 + 6) - 12 , 7 , 9 , 16.5 , 37 , ?
9297.545.2568.556.75Option B
The series is (*1 + 2) , (*1.5 + 3) , (*2 + 4) , (2.5 + 5) - 35 , 36, 40 , 49 , 65 , ?
92105759084Option D
The series is (+ 1^1) , (+ 2^2) , (+ 3^2) , (+ 4^2) , (+ 5^2) - 425 , 408 , 381 , 344 , 297 , ?
254242164240246Option D
The series is (- 17 ) , (- 27) , (- 37) , (- 47) , (- 57) - 45 , 52 , 41 , 54 , 37 , ?
5056439238Option B
The series is (+ 7) , (- 11) , (+ 13) , (- 17) , (+ 19) - 3600 , 720 , ? , 60 , 30 , 30
120180360600240Option B
The series is ( 3600 / 5 ) , ( 720 / 4 ) , ( 180 / 3 ) , ( 60 / 2 ) , ( 30 /1 ) - 4 , 5 , 12 , 39 , 160 , ?
800805482540640Option B
The series is (* 1 + 1) , (* 2 + 2 ) , (* 3 + 3 ) , ( * 4 + 4 ) , ( * 5 + 5 ) - 24 , 26 , 29 , 28 , 34 , ? , 39
3054203242Option A
The series is (24 + 5 = 29) , (26 + 2 = 28) , ( 29 + 5 = 39) , (28 + 2 = 30) …
51
Quantitative Aptitude: Time and Work Set 29
- A alone can complete a piece of work in 15 days and B & C together can complete the same work in 8 1/3 days. B is 100% more efficient than C. How many days is required to complete the work if A and C work together ?
12 days8 days6 days9 3/8 days5 daysOption D
LCM of 15 and 8 1/3 days = 75
efficiency of A = 75/15 = 5
efficiency of B and C = 75 * 3/25 = 9
let efficiency of C = 100
efficiency of B = 200
ratio of efficiency of B and C = 2 : 1
efficiency of B = 9 * 2/3 = 6
efficiency of C = 9 * 1/3 = 3
time = 75/(5 + 3) = 75/8 = 9 3/8 days - Rajat alone can complete a piece of work in ‘x’ days and Sujit alone can complete the same work in (x + 5) days. If they together can complete the same work in 6 days, then find in how days Sujit can complete the whole work ?
10 days6 days8 days5 days15 daysOption E
1/x + 1/x + 5 = 1/6
2x + 5 / x^2 + 5x = 1/6
x^2 + 5x = 12x + 30
x^2 – 7x – 30 = 0
x = 10 , – 3
Days can not come in negative, so that value of x = 10
Days taken by Sujit to complete the work = x + 5 = 15 days - A alone can complete a work in 25 days and B alone can complete same work in 45 days. How many days are taken by A and B together to complete 60% of work ?
14 days135/14 days68/7 days18/5 days9 2/5 daysOption B
LCM of 25 and 45 = 225
efficiently of A = 225/ 25 = 9
efficiently B = 225/45 = 5
days = 225/14 * 60/100 = 135/14 days - A and B can complete a work in 24 days and B and C together can complete the same work in 30 days. A and C together work for 15 days and after 15 days A and C left the work, remaining work done by alone B. If the efficiency ratio of A and B is 2 : 3, then find in how many days total work will be completed ?
28 days60 days40 days38 days25 daysOption C
LCM of 24 and 30 = 120
total work = 120
efficiency of A and B = 120/24 = 5
efficiency of B and C = 120/30 = 4
efficiency of A = 5 * 2/5 = 2
efficiency of B = 5 – 2 = 3
efficiency of C = 4 – 3 = 1
A and C together work for 15 days = (2 + 1) * 15 = 45
remaining work = 120 – 45 = 75
days required to complete remaining work = 75/3 = 25 days
total days = 15 + 25 = 40days - P , Q and R together can complete a work in 20 days and the ratio of time taken by P , Q and R is 8 : 6 : 3. How many days is taken by Q and R together to complete the whole work ?
18 days25 days26 days30 days32 daysOption B
Time ratio of P , Q and R = 8 : 6 : 3
LCM of 8, 6 and 3 = 24
efficiency ratio of P, Q and R = 24/8 : 24/6 : 24/3 = 3 : 4 : 8
let efficiency of P , Q and R = 3x , 4x and 8x respectively.
total work = 20 ( 3x + 4x + 8x ) = 300x
time taken by Q and R together complete the work = 300x / 12x = 25 days - The efficiency of Rohit is 40% more than Suraj. If Suraj alone can do a work in 14 days, then find how many days is taken by Rohit to complete the whole work ?
10 days15 days22 days13 days18 daysOption A
Efficiency of Suraj = 5x
Efficiency of Rohit = 5x * 140/100 = 7x
total work = 14 * 5x = 70x
time taken by Rohit to complete the work = 70x/7x = 10 days - A and B can do a work in 10 days B and C can do the same work in 12 days and A and C can do the same work in 15 days. How many days by A, B and C together to complete total work ?
5 days8 days14 days15 days6 daysOption B
LCM of 10 , 12 and 15 = 60
efficiency of A and B = 60/10 = 6
efficiency of B and C = 60/12 = 5
efficiency of A and C = 60/15 = 4
A + B + B + C + A + C = 15
A + B + C = 7.5
time = 60/7.5 = 8 days - 12 men do a work in 18 days. They started work together and after 8 days, 3 more joined with them. In how many days the remaining work will be completed ?
8 days9 days12 days18 days15 daysOption A
Let the remaining work completed in ‘x’ days
12 * 18 = (12 * 8) + (15 * x)
15x = 120
x = 8 days - Rita , Gita and Sita can do a piece of work in 24 days , 20 days and 15 days respectively. If they got total wages of rs. 3800, then find difference between the wages got by Sita and Gita.
500800480400620Option D
LCM of 24 , 20 and 15 = 120
total work = 120
efficiency of Rita = 120/24 = 5
efficiency of Gita = 120/20 = 6
efficiency of Rita = 120/15 = 8
difference = 3800 * 8 – 6/19 = rs.400 - If 12 men can complete a piece of work in 20 days and 15 women can complete the same work in 24 days, then in how many days 8 men and 8 women can complete the whole work ?
15 days18 days17 days12 days24 daysOption B
12 men * 20 days = 15 women * 24 days
m/w = 3/2
total work = 12 * 3 * 20 = 720
time = 720 / (8 * 3 + 8 * 2 ) = 720/40 = 18 days
52
Quantitative Aptitude: Problems on Ages Set 22
- A person is 30 years older than his son . After 6 years , the age of that person is four times the age of son that time. What is age of his son after 10 years from now ?
14 years16 years18 years18 years14.5 yearsOption A
Let the age of his son = x
age of person = x + 30
after 6 years ,
4 (x + 6) = x + 30 + 6
3x = 12
x = 4
age of son after 10 years = 10 + 4 = 14 years - The sum of age of A and B is 38 years. After 8 years the age of B is 2 years more than A. What is the age of B before 5 years ?
13 years14 years15 years20 years18 yearsOption C
Let the age of A = x years
age of B = (38 – x) years
after 8 years,
(38 – x + 8) – (x + 8) = 2
x = 18
age of B before 5 years = 38 – x – 5 = 15 years - The age of B is 8 years more than A, the age of C is 11 years less than B and the age of A is 5 years less than D. If the sum of age of A , B ,C and D is 70 years, then find the sum of age of A and B after 2 years ?
40 years15 years45 years38 years23 yearsOption D
Let the age of D = x years
the age of A = (x – 5) years
the age of B = ( x – 5 + 8 ) = x + 3 years
the age of C = (x + 3 – 11) = x – 8 years
total sum of age of A , B ,C and D = 70
x + ( x – 5) + (x +3) + (x -8) = 70
4x – 10 = 70
x = 20 years
The age of A = 20 – 5 = 15 years
The age of B = 20 + 3 = 23 years
sum = 15 + 23 = 38 years - The age of son is one-third of his father. If after 5 years the age of father and son becomes 5 : 2, then find the sum of age of father and son.
50 years60 years55 years45 years46 yearsOption B
Let the age of father = 3x
the age of son = x
after 5 years,
3x + 5/x + 5 = 5/2
6x + 10 = 5x + 25
x = 25
sum = 3x + x = 4x = 4 * 15 = 60 years - The average present age of A , B and C is 30 years and the ratio between the present age of A and C is 4 : 5. If the age of B is 8 years less than the age of C, then what is age of B after 2 years ?
26 years29 years23 years25 years30 yearsOption B
Let the A and C 4x and 5x respectively
the age of B = 5x – 8
total age of A , B and C = 30 * 3 = 90 years
4x + 5x + 5x – 8 = 90
14x = 98
x = 7
the age of B after 2 years = (5x – 8) + 2 = 29 years - The sum of present age of A , B and C is 52 years and the age of A is 3/5th of age of B. If after 11 years the age of B is equal to the three times the present age of C, then find present of C ?
26 years28 years30 years14 years25 yearsOption E
Let the present age of B = 5x
the age of A = 3x
Let the present of C = y years
5x + 11 = 3y
y = 5x + 11/3
3x + 5x + (5x + 11)/3 = 52
9x + 15 x + 5x + 11 = 156
29x = 145
x = 5
the present age of B = 5 * 5 = 25 years - 10 years ago P was half of Q in age . At present the ratio of their ages is 3 : 4. Find the sum of their ages after 3 years.
46 years35 years62 years41 years52 yearsOption D
10 years ago , let the age of Q = 2x
and the age of P = x
at present , the age of P = x + 10
the age of Q = 2x + 10
x + 10/2x + 10 = 3/4
6x + 30 = 4x + 40
2x = 10
x = 5
sum of their ages after 3 years = 2x + 13 + x + 13 = 23 + 18 = 41 years - The age of father is 40% more then his son. After 5 years the age of father is 16 years more than the age of son. Find the present age of father.
4556425856Option E
Let age of son = 5x
and father age = 5x * 140/100 = 7x
after 5 years,
(7x + 5) – (5x + 5) = 16
2x = 16
x = 8
the age of father = 7x = 7 * 8 = 56 years - The difference between the present age of A and B is 20 years. After 3 years their ages are in the ratio 9 : 19. Find the present age of B.
40 years35 years26 years14 years46 yearsOption B
Let present age of A = x years
present age of B = x + 20 years
after 3 years, the age of A = x + 3
the age of B = x + 23
x + 3 / x + 23 = 9/19
19x + 57 = 9x + 207
10x = 150
x = 15
the age of B = 15 + 20 = 35 years - The present age of father is 5 times that of his son. After 4 years he will be 4 times that of his son. Find the age of father 3 years ago.
34 years56 years42 years57 years48 yearsOption D
Let the age of son = x years
the age of father = 5x years
After 4 years,
the age of son = x + 4
the age of father = 5x + 4
4 (x + 4) = 5x + 4
4x + 16 = 5x + 4
x = 12 years
the age of father 3 years ago = 5 * 12 – 3 = 57 years
53
Quantitative Aptitude: Partnership Set 24
- A started a business by investing rs.45000. After 6 months B joined business with rs.35000 and profit of the business at the end of the year is rs. 17500. What is profit share of B ?
480052504900120008500Option C
Profit sharing ratio of A and B = (45000 * 12) : (35000 * 6 ) = 18 : 17
total profit = 17500
profit of B = 17500 * 7/25 = 4900 - Three friends A , B and C started a business by investing capital in the ratio of 3 : 4 : 6 for time period of 2 : 5 : 6. What is their profit sharing ratio ?
5 : 4 : 32 : 3 : 43 : 10 : 83 : 4 : 810 : 5 : 18Option C
Let capital invested A , B and C are 3x and 4x and 6x respectively
Profit sharing ratio = (3x * 2) : (4x * 5) : (6x * 6 )
= 6x : 20x : 36x = 3 : 10 : 18 = 3: 10 : 18 - A , B and C enters into a partnership with a total capital of rs.17400. Capital of C is rs.1400 less than capital of A and capital of C rs.200 more than the capital of B. If at the end of the year total profit of the business is rs.3480, then find difference between profit share A and B ?
540380340320400Option D
Let capital of A = x
capital of C = x – 1400
capital of B = x – 1400 – 200 = x – 1600
x + x – 1400 + x – 1600 = 17400
3x = 20400
x = 6800
capital of A = 6800
capital of B = 6800 – 1600 = 5200
capital of C = 6800 – 1400 = 5400
ratio = 6800 : 5200 : 5400 = 34 : 26 : 27
difference = 3480 * 8/87 = 320 - A and B entered into a partnership business by investing rs.8000 and rs.5000 for x months and (x + 2) months respectively. Total profit of the business at the end of the year is rs.3300 and profit share of A is 300 more than profit share of B. Find for how many months A invested capital ?
8 months5 months2 months9 months6 monthsOption E
Investment ratio of A and B = 8000 : 5000 = 8 : 5
profit sharing ratio of A and B = 8 * x : 5 ( x + 2) = 8x : 5x + 10
8x – (5x + 10)/13x + 10 = 300/3300
3x – 10 /13x + 10 = 1/11
33x – 110 = 13x + 10
20x = 120
x = 6
A invested his capital for 6 months - Ram , Shiva and Hari started a business with capital in the ratio of 8 : 6 : 5. After 8 months Ram withdrawal 25% of capital while Hari increased 20% of his investment . If at the end of the year total profit of business is rs. 14000, then what is the the profit share of Hari ?
600040008000120007000Option B
Let amount invested by Ram , Shiva and Hari = 8x , 6x and 5x
profit sharing ratio of Ram , Shiva and Hari = (8x * 8 + 6x * 4) : (6x * 12) : (5x * 8 + 6x * 4)
= 88x : 72x : 64x
= 11 : 9 : 8
total profit = 14000
profit share of Hari = 14000 * 8/28 = 4000 - A started a business with some amount and after 4 months B joined business with rs.2400. If profit of A at the end of the year is rs.2800 out of the total profit of rs. 4200, then find how much amount invested by A ?
4300024000340002500032000Option E
Let A invested rs.x
profit sharing ratio of A and B = (x * 12) : (24000 * 8) = x : 16000
profit share of A = 2800
x / x + 16000 = 2800/4200
3x = 2x + 32000
x = 32000 - A and B started a business with capital of rs.8000 and trs.6000 respectively. After 1 1/2 years B left the business while another person C joined the business with capital of rs. 7000. If at the end of the 2 years profit share of C is rs.560 , then what is total profit of the business ?
48203240135045602480Option D
Profit sharing ratio of A , B and C = (8000 * 2) : (6000 * 1.5) : (7000 * .5) = 32 : 18 : 7
total profit of the business = 560/7 * 57 = 4560 - Amit and Suraj invested rs. 4000 and rs. 6000 for 8 months and 7 months respectively. Total profit of the business is rs.3330. If they donate 20% of profit to charity fund, after that they distribute profit in their investment ratio, then what is profit share of Suraj ?
17201240151214201250Option C
Profit sharing ratio of Amit and Suraj = (4000 * 8) : (6000 * 7) = 32 : 42 = 16 : 21
total profit = 3330
They donate to fund = 3330 * 20/100 = 666
remaining profit = 3330 – 666 = 2664
profit share of Suraj = 2664 * 21/37 = 1512 - A and B started a business with capital of rs.4800 and rs.6000 for 2 years and 1.5 years respectively. Profit share of A how much percent more or less than B ?
8%6 2/3%8 1/5%4%8.5%Option B
Profit sharing ratio of A and B = (4800 * 2) : (6000 * 1.5) = 16 : 15
percentage more = 1/15 * 100 = 6 2/3% - M and N two friends started a partnership business by investing rs.8500 and rs.7000 respectively. M invested his capital for 8 months and N invested for 7 months. If profit of M is rs.760 more than profit of N, then what is profit share of M ?
25403630450027201840Option D
Profit sharing ratio of M and N = (8500 * 8) : (7000 * 7)
= 68 : 49
profit share of M = 760/68 – 49 * 68 = 2720
54
Quantitative Aptitude: Mixture and Alligation Set 17
- In a mixture of milk and water of the volume of 80 liter the ratio of milk to water is 3: 2. How much quantity of water will be added to make mixture is equal ?
1615121820Option A
Quantity of milk in the mixture = 80 * 3/5 = 48
and water = 80 * 2/5 = 32
let “x” liter of water to be added,
48 = 32 + x
x = 16 - In what ratio must rice at rs.60 per kg be mixed with rice of rs.74 per kg, so that the mixture must be worth rs.64 per kg ?
2 : 12 : 54 : 32 : 15 : 2Option E
By using alligetion method,
60 74
64
10 4
ratio = 5 : 2 - A vessels contains 80 liters of wine, 20 liters are taken out from vessel is replaced by water and the same process is further replaced two times, then find the quantity of wine left in final solution ?
12.45 liter30.60 liter33.75 liter40.85 liter52.85 literOption C
Using the formula, wine left over = x ( x – y/x)^n
= 80 ( 80 – 20/80 )^3
= 80 ( 3/4)^3 = 80 * 27/64 = 33.75 liter
- Two alloy A and B are made of copper and zinc in the ratio of 4 : 1 and 4 : 3 respectively. If these two alloys are to be mixed to form a new alloy in which same elements are in the ratio 2 : 1, then what is ratio of alloy A and alloy B in the new alloy ?
2 : 34 ; 53 : 25 : 73 : 4Option D
By using formula
4/5 4/7
2/3
2/21 2/15
ratio = 5 : 7 - In a mixture of wine and water is in the ratio of 5 : 3. If 16 liters of mixtures taken out and replaced with water, so that the ratio of wine and water becomes 3 : 5. Find the initial quantity of wine in the mixture.
2428242512Option D
Let quantity of wine and water in the mixture is 5x and 3x respectively.
(5x – 16 * 5/8)/(3x – 16 * 3/8 + 16) = 3/5
5x – 10/3x – 6 + 16 = 3/5
5x – 10/3x + 10 = 3/5
25x – 50 = 9x + 30
16x = 80
x = 5
quantity of wine in the initial mixture = 5 * 5 = 25 liter - A vessels contains mixture in which 20% water and rest quantity is milk. If 28 liter of more water is to be added in the vessel , then quantity of water becomes 3/8th of mixture. What is the quantity of milk in the vessel initially ?
80 liters65 liters42 liters68 liters78 litersOption A
Quantity of water = 20%
quantity of milk = 80%
ratio = 80 : 20 = 4 : 1
let quantity of milk and water in the vessel is 4x and x respectively.
28 liter of water is to be added,
4x /x + 28 = 5 / 3
12x = 5x + 140
7x = 140
x = 20
quantity of milk = 4 * 20 = 80 liters - Two mixtures A and B in the ratio of juice and water are 3 : 1 and 1 : 2 respectively, mixed in the ratio of 2 : 3. If the juice in final mixture is 48 liter, then find the quantity of water in final mixture ?
252250144245320Option A
By using alligation,
3/4 1/3
2/5
1/15 7/20
ratio = 4 : 21
quantity water = 48/4 * 21 = 252 liters - A seller mixed sugar cost rs.45 per kg with sugar cost rs. 38 per kg. These mixture he sold at rs.48 per kg so that he can earn 20% profit. Find in what ratio he mixed the two types of sugar ?
4 : 36 : 72 : 51 : 22 : 3Option C
SP of mixed sugar = 48
CP of mixed sugar = 48/6 * 5 = 40
using alligetion method,
45 38
40
2 5
ratio = 2 : 5 - A container contains 60 liters of milk 6 liters of milk taken out from this container and replaced by water. This process was replaced further two times. How much amount of milk left in the container ?
38.28 liters43.74 liters24.63 liters52.68 liters42 litersOption B
Using formula,
x (x – y/x)^n
= 60 ( 60 – 6/ 60) ^3
= 60 ( 54/60)^3
= 60 * 729/1000 = 43.74 liters - The ratio of quantity of two varieties of rice of 3 : 2 is mixed. If the of variety of more quantity rice is rs. 15 and the price of the mixture is. rs.16.2 per kg, then find the price of per kg rice which is the less quantity.
1418172032Option B
Let the price of less quantity rice = x
= (15 * 3 + x * 2)/ 3 + 2 = 16.2
45 + 2x = 81
2x = 81 – 45
x = 18
55
Quantitative Aptitude: Data Sufficiency Questions Set 16
- What is perimeter of the rectangle ?
I. Perimeter of square is 84 cm and length of rectangle is equal is equal to side of square.
II. The length of rectangle is 40% more than the breadth of rectangle.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option E
From I, Side of square = 84/4 = 21cm
length of rectangle = 21
from II, let of breadth of rectangle = 5x
and length = 5x * 140/100 = 7x
from I and II both,
breadth of rectangle = 21/7x * 5x = 15
perimeter of rectangle = (21 + 15)2 = 72 cm
Both statement are required to find the answer. - What is the length of train ?
I. The train crosses a 220 meters long platform in 15 seconds.
II. The train crosses a person walking in opposite direction in 6 seconds.
Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option D
From I, Let length of train = x
speed of train = y
x + 220/y = 15
From II, Let speed of man = z km/hr
x/y + z = 6
Both statement I and II are not sufficient to calculate the answer. - What is the rate of interest ?
I. Rs. 4000 becomes rs.5200 in 2 years when invested at simple interest.
II. The same sum is invested in CI and SI for 2 years at same rate of interest and difference between CI and SI is rs.90.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option C
From I, Sum = 4000
2 years interest = 5200 – 4000 = 1200
1 years interest = 1200/2 = 600
rate of interest = 600/4000 * 100 = 15%
from II, P = 4000
difference = 90
90 = 4000 * R^2/1000^2
R = 15%
either I or II is sufficient. - What is the speed of boat in still water ?
I. Boat covers 150 km in upstream speed in 10 hours.
II. Ratio of speed of downstream and upstream is 5 : 3.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option E
From I, Upstream speed = 150/10 = 15 km/hr
from II, Let downstream speed = 5x
upstream speed = 3x
from both I and II,
downstream speed = 15/3x * 5x = 25 km/hr
speed of boat = 25 + 15 /2 = 40/2 = 20 km/hr
Both statement are required to find the answer. - In how many days B alone can do the work ?
I. A and B together can complete a work is 18 days.
II. B and C together can complete the same work in 24 days.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option D
Alone statement I and II can not find answer
from both statement I and II together
LCM of 18 and 24 = 72
efficiency of A and B = 72/18 = 4
efficiency of B and C = 72/24 = 3
Here , we can not find individual efficiency so,
from both statement I and II we can not calculate the answer. - What is the area of square ?
I. The perimeter of square is 36 cm.
II. The area of rectangle is 96 cm^2 and side of square is 3 cm less than length of rectangular.
Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option A
From I, perimeter of square is 36 cm.
side of square = 36/4 = 9 cm
area of square = 9 * 9 = 81 cm^2
From II, Area of rectangle = 96 cm^2
only from II we can not find the answer.
only statement I is sufficient. - How much profit earned selling a table ?
I. The ratio of cost price and marked price of the table is 5 : 8. After giving some discount profit percent occurred is 28%.
II. The shopkeeper is given 20% discount on MP and selling price of the table is rs.320.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option E
From I , Let CP of table = 5x
MP = 8x
profit = 28%
From II, SP = 320
discount = 20%
MP = 320/4 * 5 = 400
both From I and II,
MP = 400
CP = 400/8 * 5 = 250
profit = 320 – 250 = 70
Both I and II are sufficient to find answer. - What is profit share of C ?
I. A and B start the business with capital of rs.8000 and rs.10000 respectively.
II. After 4 months C joined the business with capital of rs.6000 and total profit at the end is rs 2200.
Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option E
From I, A and B invested rs.8000 and rs.10000 respectively.
from II, total profit = rs. 2200
C invested 6000 for 8 months
Both from I and II,
Profit sharing ratio of A, b and C = (8000 * 12) : (10000 * 12) : (6000 * 8)
= 4 : 5 : 2
profit of C = 2200 * 2/11 = 400
Both statement I and II is required to find answer. - What is the age of the mother of Rohit ?
I. The age of Rohit’s father is 3 times more than age of Rohit. After 4 years the ratio of age of Rohit and his father becomes 1: 3 and the age of mother is 4 years less than the age of his father.
II. The ratio of age of Rohit and his mother is 2 : 7 and before 4 years the age of Rohit and his mother 1 : 6.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option C
From I, Let the age of Rohit = x
the age of his father = 3x + x = 4x
After 4 years,
x + 4/ 4x + 4 = 1/3
3x + 12 = 4x + 4
x = 8
age of his father = 4x = 4 * 8 = 32
age of his mother = 32 – 4 = 28
From II, Let the age of Rohit = 2x
the age of his mother = 7x
before 4 years,
2x – 4/ 7x – 4 = 1/6
12x – 24 = 7x – 4
5x = 20
x = 4
age of his mother = 7 * 4 = 28 years - How much marks scored by Rinu ?
I. Rinu scored 32% and failed by 48 marks.
II. She scored 49% which is 54 more marks than pass marks.Only statement I is sufficient.Only statement II is sufficient.Either statement I or statement II is sufficient.Neither statement I nor statement II is sufficient.Both statement I and II are sufficient.Option E
Either I or II we can not calculate the answer.
Both statement I and II,
32% + 48 = 49% – 54
17% = 102
1% = 6
pass marks = 32% + 48 = 192 + 48 = 240 marks
Both I and II is required to get answer.
56
Quantitative Aptitude: Time, Speed and Distance Set 25
- A man goes to his office at a speed of 30 km/hr and return to home at a speed of 45 km/hr. If he takes total 10 hours in all then, what is the distance between his office to home ?
120 km180 km340 km220 km200 kmOption B
Let distance = D km
D/30 – D/45 = 10
D = 180 km - The speed of car and bus in the ratio of 4 : 5. Car takes 1 hour more than bus to cover a distance of 240 km, then find speed of bus ?
40 km/hr30 km/hr60 km/hr84 km/hr72km/hrOption C
Let speed of car and bus = 4x and 5x respectively
240/4x – 240 /5x = 1
x = 12 km /hr
speed of bus = 5 * 12 = 60 km/hr - A train length of 225 meters can cross a pole in 9 sec. How much time taken by train if cross a platform whose length is 255 meters ?
22 sec19 1/5 sec12 1/2 sec18 sec20 secOption B
Speed of train = 225/9 = 25 m/sec
time = 225 + 255 / 25 = 19 1/5 sec - Ram goes to office from house at speed of 30 km/hr and reach 2 minutes before his usual time, if he goes at speed of 20 km/hr , then he reaches 3 minutes late. What is distance between office to house ?
6 km5 km12 km14 km8 kmOption B
Let distance = D
(D/20 – D/30) = 5/60 hours
D = 5 km - Train A starts from M with the speed f 80 km/hr at 10 am and B starts with the speed of 100 km/hr at 12 pm from N and total distance between M and N is 700 km, find at what time they will cross each other ?
4:00 pm3:00 pm2:00 pm5:00 pm3:30 pmOption B
Speed of train A = 80 km/hr
distance travel by train A from 10 am to 12 pm = 2 * 80 = 160 km
remaining distance = 700 – 160 = 540 km
time = 540/ (80 + 100) = 3 hours
time = 12 pm + 3 hours = 3:00 pm - 180m length of train crosses a platform at speed of 90 km/hr in 12 sec. Another train ar speed of 144 km/hr crosses same platform in 8 seconds. What is length of the other train ?
200 m400 m600 m500 m300 mOption A
Speed of train = 90 * 5 / 18 = 25 m/sec
let length of platform = x
x + 180/25 = 12
x = 300 – 180 = 120 m
let length another train = y
speed of other train = 144 * 5/18 = 40 m/sec
y + 120/40 = 8
y = 320 – 120 = 200m - two trains of length of 145 m and 215 m are running in same direction with speed of 162 km /hr and 108 km/hr respectively. How much time will they take to cross each other ?
18 seconds12 seconds15 seconds25 seconds24 secondsOption E
Speed of 145 m long train = 162 * 5/18 = 45 m/sec
speed of 215 m long train = 108 * 5/18 = 3 m/sec
time = 145 + 215/45 – 30= 360/15 = 24 sec - The sum of the length of train A and B is 700 meters and the speed of train A is 54 km/hr. If they are running in opposite direction, then they can cross each other in 20 seconds. Find the speed of train B ?
48 km/hr75 km/hr108 k/hr54 km/hr72 km/hrOption E
Speed of train A = 54 * 5/18 = 15 m/sec
total length = 700m
let speed of train B = x m/sec
700/(15 + x) = 20
x = 20 m/sec
speed of train B = 20 * 18/5 = 72 km /hr - Two stations P and Q are at a distance of 225 km. Train A starts running from station P and train B starts running from station Q respectively and meet each other after 3 hours. If the speed of train A is 5 km/hr more than the speed of train B, then find speed of train A ?
42 km/hr40 km/hr28 km/hr32 km/hr50 km/hrOption B
Let speed of train B = x km/hr
speed of train A = (x + 5) km/hr
total distance = 225 km
225/(x + 5 + x) = 3
225 = 6x + 15
x = 35
speed of train A = 35 + 5 = 40 km/hr - Sushant covers a distance by walking for 6 hours. While returning his speed decreased by 2 km/hr and he takes 9 hours to cover the same distance. What was his speed while returning ?
4 km/hr5 km/hr8 km/hr6 km/hr14 km/hrOption A
Let original speed of Sushant = x km/hr
while returning his speed = (x – 2) km /hr
x * 6 = 9 ( x – 2 )
6x = 9x – 18
x = 6
his speed while returning = 6 – 2 = 4 km/hr
57
Quantitative Aptitude: Simple/Compound Interest Set 23
- A sum of rs.P invested on compound interest annually at certain rate of interest and it three times itself in five years. In how many years the amount to 9 times itself at the same rate of interest ?
5 years8 years7 years10 years12 yearsOption D
3P = P(1 + R/100)^5
3 = (1 + R/100)^5
3^2 = (1 + R/100)5*2
9 = (1 + R/100)^10
time = 10 years - A lends rs. 5500 to B at 20% per annum and B lends the same sum to C at 22% per annum. Find the gain of B after 2 years in simple interest.
380275220440554Option C
B gives the interest to A after 2 years,
5500 * 20/100 * 2 = 2200
C gives the interest to B after 2 years
5500 * 22/100 * 2 = 2420
the gain of B = 2420 – 2200 = 220 - Difference between compound interest and simple interest on sum of rs.4800 at certain rate of interest after 2 years is rs. 108. What is the rate of interest ?
14%15%17%12.5%24%Option B
CI – SI = PR^2/100^2
108 = 4800R^2/10000
R^2 = 108 * 10000/4800
P^2 = 225
R = 15% - After two years ratio between simple interest to principle is 2 : 5. If difference between CI and SI after two years is 208, then find principle ?
48004750454048505200Option E
Let principle = 5x
and SI = 2x
rate of interest for two years = 2x/5x * 100 = 40%
rate of interest for 1 years = 40%/2 = 20%
CI – SI = PR^2/100^2
208 = P (20)^2/10000
P = 5200 - Two persons P and Q invested rs. (x + 3400) and (x+ 2200) at the rate of 15% and 20% respectively for two years in simple interest. After two years total SI is rs.7220, then how much amount invested by Q ?
76009820584064509240Option A
(x + 3400) * 15 /100 * 2 + (x + 2200) * 20/100 * 2 =7220
(x + 3400) * 3/10 + (x+2200)*2/5 = 7220
(3x + 102000/10) + (2x + 4400/5) = 7220
(3x + 10200 + 4x + 8800/10) = 7220
7x + 19000 = 72200
x = 7600 - Total sum of rs.4740 is invested by two friends A and B in a scheme at the rate interest of 12% p.a for 4 year in SI. If interest received by B is 67.20 more than interest received by A, then find how much amount invested by A ?
2800230018402350none of theseOption B
A invested = x
B invested = 4740 – x
(4740 – x) 12/100 * 4 – x * 12/100 * 4 = 67.20
48/100 ( 4740 – x – x) = 6720
12/25 (4740 – 2x) = 67.20
4740 – 2x = 67.20 * 25/12
4740 – 2x = 140
2x = 4600
x = 2300
amount invests by A= 2300 - What is the compound interest accrued on a sum of 1400 at the rate of 6% in 2 years ?
184.25254.08334.05173.04234.14Option D
Compound interest for 2 years
6 + 6 + 6 * 6/100 = 12.36 %
compound interest = 1400 * 12.36/100 = 173.04 - The compound interest on a certain sum at 20% p.a for 2 years is rs. 98 more than the simple interest on same sum at 15% per annum for 2 years. What is the sum ?
7004803201000650Option A
Let sum is rs.x
compound interest for 2 years at 20 % p.a
20 + 20 + 20 * 20 /100 = 44%
simple interest for 2 years at 15 % = 15% * 2 = 30%
x * 44/100 – x * 30/100 = 98
x = 700 - A certain sum is deposited at rate of 40% p.a on Compound interest. Difference between interest earned at the 1st and 2nd year is rs.384. What is the sum ?
48004500320045002400Option E
Let sum = 100x
interest of 1st year = 100x * 40/100 = 40x
total amount at the end of the 1st year = 100x + 40x = 140x
interest of 2nd year = 140x * 40/100 = 56x
difference = 56x – 40x = 16x
16x = 384
x = 24
sum = 100x = 100 * 24 = 2400 - What is difference between the compound interest on rs.4000 for 1.5 years at 40% p.a compounded yearly and half-yearly ?
182192534314208Option B
Rate of interest after 1.5 years compounded yearly at 40%p.a
40 + 20 + 800/100 = 68%
CI = 4000 * 68/100 = 2720
Rate of interest after 1.5 years compounded half-yearly
rate of interest = 40/2 = 20%
20 + 20 + 20 * 20 /100 = 44%
44% + 20% + 880/100 = 72.80%
CI = 4000 * 72.80 /100 = 2912
difference = 2912 – 2720 = 192
58
Quantitative Aptitude: Probability Questions – Set 23
- Two dice are rolled randomly. Find the probability to get sum is 10.
2/5142/91/125/8Option D
Required = (6 , 4 ) , (4 , 6) , ( 5, 5) = 3
total = 6 * 6 = 36
probability = 3/36 = 1/12 - Two dices are rolled out together, then what is the probability of getting a number of one dice greater than the number of other dice ?
2/31/63/81/85/6Option E
Non-favorable events = (1 , 1) , (2 , 2) , (3 , 3) , (4 , 4) , (5 , 5) , (6,6) = 6
total = 6 * 6 = 36
probability of non-favorable events = 6/36 = 1/6
probability of favorable events = 1 – 1/6 = 5/6 - If 2 cards is drawn at randomly from 52 cards, then find the probability of getting both are red cards.
13/2826/10528/10825/102none of theseOption D
Required = 26C2 = 26 * 25/2 = 13 * 25
total = 52C2 = 52 * 51 / 2 = 26 * 51
probability = 13 * 25 / 26 * 51 = 25 /102 - In how many ways, we can arrange the letters of the word ‘LIGHT’ ?
8428140160120Option E
Ways = 5! = 5 * 4 * 3 * 2 * 1 = 120 - In how many different ways, we can arrange the letters of the word ‘MOUSE’ , so that the middle position is always occupied by ‘S’ ?
2524484268Option B
Ways = 4! = 4 * 3 * 2 * 1 = 24 - How many ways 6 books can be selected from 14 different books , if two particular books are always selected ?
495480231384520Option A
Available objects = 14 – 2 = 12
Ways = 12C4 = 12 * 11 * 10 * 9/4 * 3 * 2 * 1 = 495 - A bag contains 2 white balls, 3 pink balls and 2 black balls. 2 balls are drawn randomly. What is the probability that there is no black balls ?
8/2110/211/83/56/11Option B
Required = 5C2 = 5*4/2 = 10
total = 7C2 = 7 * 6 / 2 = 21
probability = 10/21 - When two coins are tossed simultaneously, then find the probability of getting at least one tail.
533/41/42/5Option C
Required = ( 1 head , 1 tail ) , ( 2 tails) = (2C1) + (2C2) = 2 + 1 = 3
total = 2^2 = 4
probability = 3/4 - A bag contains 4 red balls, 2 blue balls and 2 green balls . If two balls are drawn randomly from the bag , then find the probability of getting both balls of different color.
2/75/85/748Option C
probability = 4C1 * 2C1 / 8C2 + 4C1 * 2C1 / 8C2 + 2C1 * 2C1 / 8C2
(4 * 2 * 2)/ 8 * 7 + (4 * 2 * 2)/ 8 * 7 + (2 * 2 * 2) / 8 * 7 = 2/7 + 2/7 + 1/7 = 5/7 - A group of students sitting around a rectangular table, find probability of 2 specified students sitting together.
3/82/78/73/86/11Option B
Favorable cases = 6! * 2!
total cases = 7!
probability = 6! * 2! /7! = 2/7
59
Quantitative Aptitude: Data Interpretation Questions Set 155
Directions : The given below table shows that the number of boys and girls studied in five different classes.
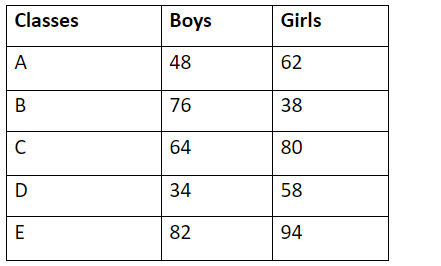
- No. of boys in class A and B together is how many more or less than no. of girls in class C and E together ?
6538524850Option E
Total no. of boys in class A and B = 48 + 76 = 124
total of no. of girls in class C and E = 80 + 94 = 174
difference = 174 – 124 = 50 - What is the ratio of total no. of girls in class B and no. of boys in class D ?
17 : 1915 : 196 : 53 : 419 : 17Option E
Ratio = 38 : 34 = 19 : 17 - No. of boys in class A and C together is what percent more or less than than the no. of girls in class C ?
50%40%46%56%64%Option B
Total no. of boys in class A and C together = 48 + 64 = 112
girls in class C = 80
percentage = more = 112 – 80 / 100 = 40% - What is difference between total no. of students in class D and total no. of students in class A ?
1825344652Option A
Total students in class D = 34 + 58 = 92
total students in class A = 48 + 62 = 110
difference = 110 – 92 = 18 - Total no. of students in class F is 20% more than the total no. of students in class A. If ratio of boys and girls in class F is 2 : 1 , then find total no. of boys in class F and E together.
125170280240270Option B
Total students in class A = 110
total students in class F = 110 * 6/5 = 132
boys in class F = 132 * 2/3 = 88
total boys in class F and E = 88 + 82 = 170
Difference between total marks scored by Ram in Math and Economics together to total marks scored in English and Chemistry together ?3546685482Option D
Total marks in Math and Economics together = 1800 * (20% + 15%)/100 = 630
Total marks in English and Chemistry together = 1800 * (10% + 22%)/100 = 576
difference = 630 – 576 = 54- What is the ratio between marks scored by Ram in Physics and in Economics ?
3 : 21 : 52 : 35 : 42 : 5Option D
Ratio = 25% : 20% = 5 : 4 - Total marks scored in Math is what percent more or less than total marks scored in History ?
67.5%28.4%87.5%92.25%50%Option C
Percentage = 15% – 8% / 8% = 100 = 87.5% - Total marks scored by Ram in Physics and Math together how much more or less than total marks scored in History and Economics together ?
220320540216175Option D
Total marks in Physics and Math together = 1800 * (15 + 25)/100 = 720
Total marks in Physics and Economics together = 1800 * (20 + 8)/100 = 504
Difference = 720 – 504 = 216 - What is the central angle of marks scored by Ram in English ?
82 degree36 degree144 degree72 degree40 degreeOption B
Central angle = 10/100 * 360 = 36 degree
Directions : The following pie-chart given below shows that the percentage distribution marks of six different subjects scored by Ram.
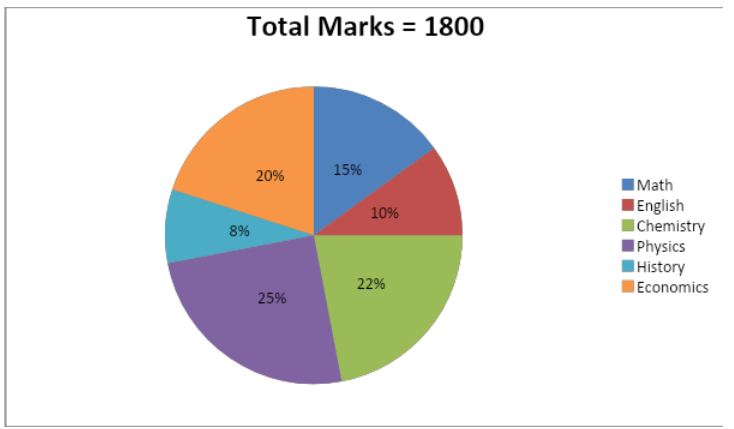
60
Quantitative Aptitude: Mensuration Questions Set 17
- What is the area of a tringle whose sides are 7cm and 9cm ?
18 √242 √612 √25 √312 √5Option E
S = 7 + 8 + 9/2 = 24/2 = 12
Area of tringle = √ S(S – a) (S – b) (S – c)
= √ 12 * 5 * 4 * 3
= 12 √ 5 - The perimeter of a square is 96 cm. If the radius of a circle is 3 cm less than the side of that square, then what is area of the circle ?
1280134598010451386Option E
perimeter of square = 96cm
side of square = 96/4 = 24cm
radius of circle = 24 – 3 = 21 cm
area of circle = πr^2 = 22/7 * 21 *21 = 1386 cm^2 - The area of a rectangular field is 252cm^2 and ratio between length and breadth is 9 :7. If cost of wire which is to be fenced is rs.2 per meter, then find cost of fencing the field ?
240340130145128Option E
Let length and breadth are 9x and 7x respectively.
9x * 7x = 252
x = 2
length = 9 * 2 = 18
breadth = 7 * 2 = 14
perimeter of rectangular field = 2(18 + 14) = 64m
cost of fencing wire = 64 * 2 = 128 - The perimeter of rectangle is 72m and ratio between the length and breadth is 11 : 7. What is the difference between the half of the length and one-seventh of the breadth of rectangle ?
9m6m12m15m17mOption A
Let length and breadth of rectangle 11x and 7x respectively.
perimeter = 72m
2(11x + 7x) = 72
x = 2
length = 11 * 2 = 22
breadth = 7 * 2 = 14
difference = 22/2 – 14 * 1/7 = 11 – 2 = 9m - There are two circle A and B and diameter of circle A is equal to be the radius of circle B,. If radius of circle A is 14 cm, Then find the difference between the perimeter of two circle ?
48cm42cm154cm88cm28cmOption D
Radius of circle A = 14 cm
Diameter of circle A = 14 * 2 = 28
radius of circle B = 28
perimeter of circle A = 2 * 22/7 * 14 = 88cm
perimeter of circle B = 2 * 22/7 * 28 = 176 cm
difference = 176 – 88 = 88cm - Curved surface area of a cylinder is 2640 cm^2 and its height is 20cm. Find the volume of a cylinder.
27720 cm^24840 cm^222350 cm^232430 cm^216340 cm^2Option A
C.S.A = 2640
2πrh = 2640
2 * 22/7 * r * 20 = 2640
r = 2640 * 7 / 44 * 20 = 21
volume = πr^2h = 22/7 * 21 * 21 * 20 = 27720 cm^2 - The length of the rectangle A is 4 m more than the breadth of rectangle and perimeter of rectangle A is 56m. What is the area of rectangle B whose length is equal to the length of rectangle A and breadth is 8 m ?
64 m^248 m^224 m^2128 m^2120 m^2Option D
Let breadth of rectangle A = x
length = x + 4
perimeter = 56
2(x + x + 4) = 56
4x + 8 = 56
x = 12
length of rectangle A = 12 + 4 = 16
length of rectangle B = 16
breadth = 8
area = 16 * 8 = 128 m^2 - A trapezium whose parallel sides are 18 cm and 14 cm long and distance between them ids 9cm. What is the area of trapezium ?
158 cm^2240 cm^2144 cm^2152 cm^2245 cm^2Option C
Area of trapezium = 1/2 * (18 + 14) * 9 = 144 cm ^2 - If the ratio of two curved surface area of two cylinder A and B are 4 : 5 and ratio of their radius is 2 : 1, then what is the ratio of their volumes ?
8 : 79 : 1013 : 78 : 53 : 4Option D
Let radius of cylinder A and B = r_1 and r_2
height cylinder A and B = h_1 and h_2
2πr_1 h_1 / 2πr_2 h_2 = 4/5
h_1 / h_2 * 2/1 = 4/5
h_1 / h_2 = 2/5
ratio of their volumes = π^2r_1 h_1 / π^2r_2 h_2
(2)^2 * 2 / (1)^2 * 5 = 8/5 - If the radius of cone is increased by 50% and height is decreased by 40%, then find the percentage change in the volume ?
55% decrease40% increase45% decrease48% increase50% decreaseOption A
Let radius of cone = 100
after increased radius of cone = 100 + 50 = 150
ratio = 2 : 3
let height of cone = 100
after decreased radius of cone = 100 – 40 = 60
ratio = 5 : 3
volume = 1/3 * πr^2h = 1/3 * 22/7 * 4 * 5 = 440 / 21
volume = 1/3 * πr^2h = 1/3 * 22/7 * 3 * 3 = 198/21
decrease = 242 / 440 * 100 = 55%
61
Quantitative Aptitude: Probability Questions – Set 22
- Two dice are rolled randomly. Find the probability to get sum is 10.
2/5142/91/125/8Option D
Required = (6 , 4 ) , (4 , 6) , ( 5, 5) = 3
total = 6 * 6 = 36
probability = 3/36 = 1/12 - Two dices are rolled out together, then what is the probability of getting a number of one dice greater than the number of other dice ?
2/31/63/81/85/6Option E
Non-favorable events = (1 , 1) , (2 , 2) , (3 , 3) , (4 , 4) , (5 , 5) , (6,6) = 6
total = 6 * 6 = 36
probability of non-favorable events = 6/36 = 1/6
probability of favorable events = 1 – 1/6 = 5/6 - If 2 cards is drawn at randomly from 52 cards, then find the probability of getting both are red cards.
13/2826/10528/10825/102none of theseOption D
Required = 26C2 = 26 * 25/2 = 13 * 25
total = 52C2 = 52 * 51 / 2 = 26 * 51
probability = 13 * 25 / 26 * 51 = 25 /102 - In how many ways, we can arrange the letters of the word ‘LIGHT’ ?
8428140160120Option E
Ways = 5! = 5 * 4 * 3 * 2 * 1 = 120 - In how many different ways, we can arrange the letters of the word ‘MOUSE’ , so that the middle position is always occupied by ‘S’ ?
2524484268Option B
Ways = 4! = 4 * 3 * 2 * 1 = 24 - How many ways 6 books can be selected from 14 different books , if two particular books are always selected ?
495480231384520Option A
Available objects = 14 – 2 = 12
Ways = 12C4 = 12 * 11 * 10 * 9/4 * 3 * 2 * 1 = 495 - A bag contains 2 white balls, 3 pink balls and 2 black balls. 2 balls are drawn randomly. What is the probability that there is no black balls ?
8/2110/211/83/56/11Option B
Required = 5C2 = 5*4/2 = 10
total = 7C2 = 7 * 6 / 2 = 21
probability = 10/21 - When two coins are tossed simultaneously, then find the probability of getting at least one tail.
533/41/42/5Option C
Required = ( 1 head , 1 tail ) , ( 2 tails) = (2C1) + (2C2) = 2 + 1 = 3
total = 2^2 = 4
probability = 3/4 - A bag contains 4 red balls, 2 blue balls and 2 green balls . If two balls are drawn randomly from the bag , then find the probability of getting both balls of different color.
2/75/85/748Option C
probability = 4C1 * 2C1 / 8C2 + 4C1 * 2C1 / 8C2 + 2C1 * 2C1 / 8C2
(4 * 2 * 2)/ 8 * 7 + (4 * 2 * 2)/ 8 * 7 + (2 * 2 * 2) / 8 * 7 = 2/7 + 2/7 + 1/7 = 5/7 - A group of students sitting around a rectangular table, find probability of 2 specified students sitting together.
3/82/78/73/86/11Option B
Favorable cases = 6! * 2!
total cases = 7!
probability = 6! * 2! /7! = 2/7
62
Quantitative Aptitude: Number Series Set 154
- 32, 80, 200, 500, 1250 ?
31254125250037505125Option A
The series is (32*2.5), (80*2.5), (200*2.5)….. - 12, 29, 63, 131, 267, ?
541538429539342Option D
The series is (*2+5), (*2+5)… - 48, 51, 56, 63, ?, 87
7274757876Option B
The series (+3), (+5), (+7), (+11), (+13) the addition of prime numbers. - 1248, 1184, 1135, 1099, 1074, ?
115853810581220625Option C
The series (-8^2), (-7^2), (-6^2)… - 6420, 6435, 6465, 6510, ?, 6645
64206500653065706424Option D
The series is (+15), (+30), (+45)… - 8, 8, 12, 28, 88, 932
2888932128Option B
The series is (*.5+4), (*1+4), (*2+4), (*4+4), (*8+4) - 320, 330, 310, 340, 300, 360
300360340320310Option B
The series is (+10), (-20), (+30), (-40), (+50) - 32, 33, 41, 68, 114, 257
257684111433Option D
The series is (+1^3), (+2^3), (+3^3), (+4^3), (+5^3 ) - 18, 36, 108, 432, 2160, 12360
12360216043210836Option A
The series is (*2), (*3), (*4)… - 45, 49, 41, 45, 37, 42
4549414237Option D
The series is (+4), (-8), (+4), (-8), (+4)
63
Quantitative Aptitude: Partnership Set 23
- Three partners A,B and C undergo a partnership. Their investment are rs.2500, rs.30000 and rs.45000 for a time period of 4years, 3years and 2years respectively, find the ratio of their profit ?
15:8:710:9:95:4:38:7:5none of theseOption B
The ratio are their profit =
25000*4:30000*3:45000*2
=100000:90000:90000
=10:9:9 - Sakti stands business with rs.5000 and after 6 months Sagar joins with Sakti as his partner. After a year the profit are divided in the ratio of 4:5 How much did Sagar contribute ?
140009500100001350012500Option E
Let Sagar contributes in business =x
profit ratio= 4:5
(5000*12)/x*6=4/5
24x=300000
x =12500 - P,Q,R invested capitals in the ratio of 3:4:7. The timing of their investment being in the ratio of 4:6:3. What ratio would their profits be distributed ?
4:8:77:8:99:9:92:3:7none of theseOption A
let the capitals invested by P,Q,R be 3x, 4x, 7x respectively
and timing of their investments be 4y, 6y, 3y respectively
profit ratio of P, Q, R=(3x*4y):(4x*6y):(7x*3y)
=12xy:24xy:21xy
=4:8:7 - A is working partner and B is a sleeping partner. A puts in rs. 10000 and B puts 12000. A received 12.5% of profit for managing the business and rest is divided in proportion to their capitals. What is A’s share of profit in a profit of rs.880 after a year.
540380460480500Option C
A’s share for managing the business=12.5% of 880=110
remaining profit=880-110=770
profit ratio of A and B= 10000:12000=5:6
A’s share=770*5/11=350
A’s total profit=110+350=460 - C and D started a business with initial investments in the ratio of 9:10 and their annual profits were in the ratio of 3:5. If C invested the money for 8 months, for how many months did D invests his money ?
12 months10 months11 months8 months6 monthsOption A
let D invests his money for x months
ATQ, (9*8)/10*x=3/5
30x=360
x=12 months - Meena started a business investing rs.12000. After 4 months Leena joined her with a capital of rs.15000 at the end of the year the total profit was rs.4400. What is the share of profit of Meena ?
36002000300024003200Option D
Profit ratio of Meena and Leena
= 12000*12:15000*8
=144000:120000
=6:5
Meena’s profit share = 4400*6/11
=2400 - Amit and Sumit invested rs.2000 and rs.3000 respectively in a partnership. After 1 year Sumit increased his amount by 33.33% and at the end of the 3 years, difference between his profit share is rs.500 .Find the profit share of sumit.
120011008001000700Option B
Ratio of profit share of Amit and Sumit
=(2000*3):(3000*1+4000*2)
=6000:11000 =6:11
Difference of profit share =500
profit share of sumit =500/5*11 =1100 - P and Q invested total rs.8000 in business and ratio of time period for which P and Q invested is 3:2. If they got total profit of rs.3600 and profit share of P is rs.1200, then find investment of Q ?
50006000400030004500Option B
Let P’s invested =x
Q’s invested = 8000-x
ratio of their time =3:2
3x/2(8000-x) =1200/2400
3x/16000-2x =1/2
6x = 16000-2x
8x =16000
x =2000
invested by Q =8000-2000 =6000 - Miki and Liza entered into partnership by investing rs.6000 and rs.7000 respectively. Period of investment of Miki and Liza is 5 months and x months respectively. In at the end of the year, Miki received rs.30000 as profit out of total profit of rs.72000, then find x.
5 months6 months8 months4 months2 monthsOption B
Profit ratio of Miki and Liza =6000*5:7000*x
30:7x
Miki’s profit =30000
Liza’s profit =72000-30000
= 42000
30/7x =30000/42000
7x =42
x= 6months . - Deepak and Dinesh invested rs.25000 and rs.50000 respectively in a business. If Dinesh invested for 8 months and total profit at the end of the year is rs.63000, then find profit share of Deepak.
2000048000250004000027000Option E
profit sharing ratio of Deepak and Dinesh=(25000*12):(50000*8)=3:4
total profit=63000
Deepak’s profit share=63000*3/7=27000
64
Quantitative Aptitude: Ratio and Proportion Questions Set 12
- In a mixture of 80 liters, the ratio of milks and water is 3:2 . How much water must be added to this mixture so that the ratio of milk and water becomes 3:4.
2428403632Option E
Total mixture =80 liters.
milk =80*3/5 =48
water =80*2/5 =32
Let, x liters of water is added.
48/32+x =3/4
32+x =64
x =64-32 =32 liters. - In a school the students of three classes are in the ratio of 2:3:5 . If 20 students are increased in every class the ratio of changes is 4:5:7. What is the total number of students in the three classes before the class increased .
200100250300400Option B
Let students in three classes be
2x, 3x and 5x respectively.
According to the question ,
(2x+20):(3x+20):(5x+20) =4:5:7
2x+20/3x+20 =4/5
12x+80 =10x+100
2x=20
x=10
Total students =(2*10)+(3*10)+(5*10)
= 20+30+50 =100 - If 16 cows cost as much as 8 bullocks, 10 bullocks cost as much as 5 horses and 3 horses cost as much as 4 camels. If the cost of one camel is rs.3300. Find the cost of one cow is,
21002200230011001200Option D
1 camel cost=3300
4 camel cost=13200
3 horses cost=13200
1 horses cost=4400
5 horses cost=22000
10 bullocks cost=22000
1 bullocks cost=2200
8 bullocks cost =17600
16 cows cost =17600
1 cows cost =1100 - The ratio of the earning of A and B is 3:5. If the earning of a increased by one-forth and the earning of B decreased by one-forth, then find the new ratio of their earning ?
2:31:13:45:22:5Option B
Let earning of A and B be 3x and 5x.
New ratio of their earning = 3x*5/4:5x*3/4 =1:1 - A some of money is to be distributed among A,B,C,D in the proportion of 3:5:2:4 . If D gets 3000 more than C, then find total money which is distribute among all.
3000021000250002800024000Option B
Let the money is distributed among A,B,C and D be 3x,5x,2x and 4x respectively.
4x-2x =3000
2x =3000
x =1500
total amount of money distributed =3x+5x+2x+4x =14x
= 14*1500 =21000 - The ratio of the number of boys and girls in a college is 7:9. If the percentage increase in the number of boys and girls be 20% and 30% respectively. The total number of boys and girls in college before increase is 1440, then find ratio of boys and girls in the college after increased.
28:3938:4325:2835:2830:37Option A
ratio of boys and girls=7:9
total boys and girls=1440
boys=1440*7/16=630
girls=1440*9/16=810
the number of boys after increased=630*120/100=756
the number of girls after increased=810*130/100=1053
ratio of boys and girls after increased=756:1053=28:39 - Salaries of Ram and Rohit are in the ratio of 4:5. If the salary of each is increased by rs.3000, the new ratio becomes 10:11. What is initial salary of Rohit.
27003000420025003500Option D
let salaries of Ram and Rohit be 4x and 5x
(4x+3000)/(5x+3000)=10/11
44x+33000=50x+30000
6x=3000
x=500
initial salary of Rohit=5x=5*500=2500 - A contains a mixture of 56 liters of wine and water in the ratio of 3:4 . If 28 liter of mixture is taken and 8 liter of wine is added , then find the ratio of new mixture .
3:28:35:55:43:4Option D
Ratio of wine and water =3:4
wine =56*3/7 =24
water =56*4/7 =32
28 liter of mixture taken out wine = 24-(28*3/7) =24-12 =12
water=32-(24*4/7) =32-16 =16
8 liters of wined is added then ,
new ratio of wine and water =(12+8):16 =20:16 =5:4 - 48% of A is equal to 64% of B, then find the ratio of A and B ?
3:23:47:35:44:3Option E
48% of A = 64% of B
A/B=64/48=4:3 - The ratio of three numbers is 2:4:5 and sum of their squares is 1125. Find the sum of the numbers.
6045505565Option D
ratio of three numbers=2:4:5
let the numbers be 2x, 4x and 5x
sum of their squares=1125
4x^2+16x^2+25x^2=1125
45x^2=1125
x^2=25
x=5
the sum of the numbers=2x+4x+5x=11x=11*5=55
65
Quantitative Aptitude: Number Series Set 153
- 960, 839, 758, 709, 684, ?
685550485675745Option D
the series is, (-11^2), (-9^2), (-7^2)… - 340, 356, 382, 418, 464, ?
520480540516496Option A
the series is, +16, +26, +36, +46, +56 - 15, 41, 78, 128, 193, ?
278275385345264Option B
the series is, +(5^2+1), +(6^2+1), +(7^2+1)… - 335, 351, 383, 431, ?, 575
487535530485495Option E
the series is, +16, +32, +48, +64, +80 - 13, 15, 21, 33, 53, ?
8396958580Option A
the series is, +(1*2), +(2*3), +(3*4), +(4*5), +(5*6) - 8, 18, 57, 232, 1165, 6994
11652325769948Option D
the series is, (*2+2), (*3+3), (*4+4)… - 14, 20, 32, 44, 58, 74
1420327444Option B
the series is, +8, +10, +12, +14, +16 - 244, 202, 172, 152, 140, 132
132140244172152Option A
the series is, -(6^2+6), -(5^2+5), -(4^2+4)… - 35, 44, 28, 53, 17, 65
3565175328Option B
the series is, +3^2, -4^2, +5^2, -6^2, +7^2 - 36, 23, 28, 47, 99, 252
99472825236Option D
the series is, (*.5+5), (*1+5), (*1.5+5), (*2+5), (*2.5+5)
66
Quantitative Aptitude: Quadratic Equations Questions Set 77
- x^2+14x+24 =0
y^2+18x+65 =0X>YXX≥YX≤YX=Y or no relationOption E
I. x^2+12x+2x+24 =0
x= -12, -2
II. x^2+13x+5x+65 =0
x= -13, -5 - I. 2x^2+23x++65 =0
II. 3x^2+25x+50=0X>YXX≥YX≤YX=Y or no relationOption D
I. 2x^2+13x+10x+65=0
2x=-13, -10
x=-6.5, -5
II. 3x^2+15x+10x+50 =0
3x= -15,-10
x=-5, -3.33 - I. x^2-18x+72=0
II. y^2-8y+15 =0
X>YXX≥YX≤YX=Y or no relationOption A
I. x^2-12x-6x+72=0
x =12, 6
II. y^2-5y-3y+15 =0
y=5, 3 - I. x^3= 729
II. y =√81X>YXX≥YX≤YX=Y or no relationOption E
I. x^3=729
x=9
II. y=9 - I. x^2-11x+18 =0
II. y^2-23y+132 =0X>YXX≥YX≤YX=Y or no relationOption B
I. x^2-9x-2x+18 =0
x=9, 2
II. y^2-12y-11y+132 =0
y^2 =12, 11 - I. 4x^2-12x+5 =0
II. 2y^2+3y-5=0X>YXX≥YX≤YX=Y or no relationOption E
I. 4x^2-10x-2x+5 =0
4x=10, 2
x= 2.5, .5
II. 2y^2+5y-2y-5 =0
2y= -5, 2
y= -2.5, 1 - I. x^2-3x+28 =0
II. y^2+3y-18=0X>YXX≥YX≤YX=Y or no relationOption E
I. x^2-7x+4x+28=0
x=7, -4
II. y^2+6y-3y-18=0
y=-6, 3 - I. x^4=256
II. y^3=64X>YXX≥YX≤YX=Y or no relationOption D
I. x^4=256
x=4, -4
II. y^3=64
y=4, 4 - I. x^2-35x+250=0
Ii. y^2-14y+40=0X>YXX≥YX≤YX=Y or no relationOption C
I. x^2-25x-10x+250=0
x=25,10
II. y^2-10y-4y+40=0
y=10,4 - I. x+5=√100
II. y+8=√144X>YXX≥YX≤YX=Y or no relationOption A
I. x+5=√100
x+5=10
x=5
II. y+8=√144
y+8=12
y=4
67
Quantitative Aptitude: Simplification Questions Set 116
- Direction: What will come in place of question(?) marks in the following questions ?
13540+12981+1519-? =250004260314033403040none of theseOption D
13540+12981+1519-25000 =3040 - (1696÷4-?)10=1200
404304340420520Option B
(424-x)10 =1200
4240-10x =1200
x =304 - 19*12*8+94 =?
19182018220019001920Option A
1824+94=1918 - 120% of 55+240% of 25+? =140
1614202224Option B
66+60+? =140
?=14 - (196/27*4)*(8/20)*(180/9)*(81/7)= ?
178210180168none of theseOption D
7*8*3 =168 - Direction: What will come in place of ‘x’ in the following questions given below ?
20% of 25% of 40% of 1200 =x+82216121815Option B
1/5*1/4*2/5*1200 =x+8
x= 24-8 =16 - 52^2+62^2+75^2-85^2 =x+48
5000600052004200none of theseOption A
2704+3844+5625-7225-48 =x
12273-7225-48 =x
x =5000 - √3025+√1600-81+x=79
5564606570Option D
55+40-81+x =79
x= 65 - 520/13+980-1020/17+20% of 55 =x+88
883880920780783Option A
40+980-60+11 =x+88
x= 883 - 168÷21*8+218+x =525
345445355245280Option D
64+218+x =527
x= 527-282
x= 245
68
Quantitative Aptitude: Simplification Questions Set 115
- Directions : What will come in place of questions mark ( ? ) in the following questions ?
37.5% of 288 + 17.5% of 1600 – 292 = ?8542985696Option E
3/8 * 288 + 7/40 * 1600 – 292 = ?
108 + 280 – 292 = ?
? = 96 - 442 – 1325 + 2480 – 225 = ?
23724220137224203250Option C
2480 + 442 – 1325 – 225 = ?
2922 – 1550 = ?
? = 1372 - 54% of 5200 – 338 + 288/12 = ?
2850325034824943296Option D
2808 – 338 + 24 = ?
? = 2494 - 450 ÷ 25 + 328 + 19% of 2200 = ?
286664764280250Option C
18 + 328 + 418 = ?
? = 764 - 1520 ÷ 5 ÷ 2 * 20 + 325 = ?
82503268336552404280Option C
1520 / (5 * 2 ) * 20 + 325 = ?
3040 + 325 = ?
? = 3365 - 8^3 + 5^3 + 260 – √1024 = ?
9808651250740634Option B
512 + 125 + 260 – 32 = ?
? = 897 – 32
? = 865 - √4624 + √1296 – ∛5832 = ?
6756894586Option E
68 + 36 – 18 = ?
? = 86 - 5 2/3 + 2 1/4 – 1 1/2 = ?
3 2/55 1/42 1/53 5/66 5/12Option E
5 2/3 + 2 1/4 – 1 1/2 = ?
6 ( 8 + 3 – 6 / 12 ) = ?
? = 6 5/12 - (169 + √225) * 2 = ?
8666525642Option D
(13 + 15) * 2 = ?
? = 56 - ( 8 * 6 ÷ 12 ) * 5 + 12 = ?
3832548946Option B
8 * 6 /12 * 5 + 12 = ?
20 + 12 = ?
? = 32
69
Quantitative Aptitude: Mixture and Alligation Set 16
- In what ratio must tea at rs.36 per kg be mixed with tea at rs.40 per kg so that the mixture must be worth rs.37 per kg ?
2:15:22:33:12:2Option D
let tea at rs.36 per kg mixed=x kg
and tea at rs.40 per kg mixed=y kg
(36x+40y)x+y=37
36x+40y=37x+37y
x=3y
x:y=3:1 - A person has a chemical of rs.25 per liter. In what ratio should water be mixed in that chemical so that after selling the mixture at rs.20 per liter he may get a profit of 25% ?
15:1216:95:48:44:5Option B
CP of chemical =rs.25
CP of water=rs.0
SP of mixture=rs.20
CP of mixture=20*4/5=rs.16
ratio of chemical and water be mixed=0-16/16-25=16/9=16:9 - A vessel contains 700 liters mixture of milk and water in the ratio 4:3 respectively. If 140 liters mixture from the vessel is completely replaced with milk, then find ratio of milk to water in the final mixture in the vessel.
12:2523:1213:2823:1512:23Option B
total mixture=700
ratio of milk to water=4:3
milk=700*4/7=400
water=700*3/7=300
140 liter mixture is replace with milk
ratio=(400-140*4/7+140)/(300-140*3/7)=320+140/240=460/240=23:12 - In a 88 liters of mixture the ratio of milk and water 7:4. If x liter of water is mixed in this mixture, so that ratio of water to milk 3:4. Find the value of x.
1215102018Option C
milk in the mixture =88*7/11=56
water in the mixture=88*4/11=32
x liter of water mixed
56/32+x=4/3
42=32+x
x=10 liter - Two vessels A & B contains mixture of milk and water in the ratio of 8:7 and 3:2 respectively. If ratio of quantity of mixture in vessels A and B 6:5 and both mixed together, then find ratio of milk to water in resulting mixture.
34:2531:248:915:2824:25Option B
let total mixture in vessel A and B be 60x and 50x respectively
total milk in resulting mixture=60x*8/15+50x*3/5=32x+30x=62x
total water in resulting mixture=60x*7/15+50x*2/5=28x+20x=48x
ratio of milk and water=62x:48x=31:24 - In a mixture of 45 liters, the ratio of chemical and water is 5:4. How much chemical must be added to make the ratio of 3:2 ?
8610512Option D
chemical in the mixture=45*5/9=25
water in the mixture=45*4/9=20
let chemical added to the mixture=x
25+x/20=3/2
2x+50=60
x=5 - Ratio between milk and water in a mixture is 5:2. When 15 liters of water is added in the mixture then ratio becomes 5:3. Find the initial quantity of mixture.
1001059012095Option B
let milk in the mixture =5x
and water=2x
5x/2x+15=5/3
15x=10x+75
5x=75
x=15
initial mixture=7x=7*15=105 liters - Ratio between chemical and water in a 120 liters of mixture is 8:7. When 30 liters of mixture is taken out and 6 liter of water is added, then what will be the ratio between chemical and water in new mixture ?
2:15:43:43:11:1Option E
milk in the mixture=120*8/15=64
water in the mixture=120*7/15=56
ATQ, ratio=(64-30*8/15)/(56-30*7/15+6)
=64-16/56-14+6=48/48
=1:1 - In a vessel ratio of milk to water is 5:3. 40 liters of mixture is taken out and 20 liters of water is added so that quantity of milk in the new mixture is 10 liters more than that of water. Find initial quantity of the mixture.
180160150170120Option B
let milk and water in the mixture be 5x and 3x respectively
5x-40*5/8-(3x-40*3/8)=10
5x-25-(3x-15+20)=10
5x-2x-3x-5=10
2x-30=10
2x=40
x=20
initial mixture=8x=8*20=160 - Container A and B contains 400 liters of milk and 160 liters of water respectively. 40% of the milk and 40% of water is mixed together in a separate container. Find the ratio of milk to water in the mixture thus formed.
3:22:18:55:42:5Option D
ratio milk to water=400*40/100:160*40/100=160:64=10:8=5:4
70
Quantitative Aptitude: Number Series Set 152
- Direction: What should be come in place of question (?) mark in the given number series ?
23, 23, 27, 43, 79, 16023274379160Option E
the series is, 0^2=0 , 2^2=4, 4^2=16, 6^2=36… - 16, 9, 11, 19.5, 45, 112.5
164511919.5Option B
the series is, (*.5+1), (*1+2), (1.5+3)… - 320, 328, 344, 368, 440, 568
320344368440568Option C
the series is, +8, +16,+32, +64… - 22, 44, 88, 528, 2640, 15840
5288826404422Option B
the series is *2, *3, *4, *5… - 56, 80, 112, 136, 168, 200
56112168136200Option E
the series is, +24, +32, +24, +32… - 20, 30, 50, 80, 120, ?
170150160190200Option A
the series is, +10, +20, +30, +40, +50 - 15, 28, 48, 82, 137, ?
210220230200180Option B
the series is difference of difference. - 330, 343, 360, 379, 402, ?
431427432435440Option A
the series is, 13, 17, 19, 23, 29 difference of consecutive prime numbers. - 9600, 1920, 480, ?, 80, 80
20032080240160Option E
the series is, ÷5, ÷4, ÷3, ÷2, ÷1 - 25, 55, 85, 115, 145, ?
165160170175180Option D
the series is +30, +30, +30…
71
Quantitative Aptitude: Time and Work Set 28
- A and B can do a work together in 20 days . B and C can do the same work in 15 days C and A also can do the same work in 12 days . In how many days all together can complete the total work and also find the who of them works of the fasted speed.
20 days, B10 days, C12 days,A18 days, B15 days, COption B
LCM of 20,15 and 12 = 60
total work =60
efficiency of A and B together = 60/20=3
efficiency of B and C together = 60/15 =4
efficiency of C and A together =60/12=5
2A+2B+2C =12
(A+B+C)’s total efficiency = 6
A,B and C together complete the work =60/6 =10 days .
A’s efficiency =6-4 =2
B’s efficiency= 6-5 =1
C’s efficiency=6-3 = 3
C works at the fastest speed. - A works at half the speed of B and C works at double the speed of B . If they all together can do a work in 40 days. In how many days will A and C complete the same work together ?
6056586570Option B
Let,
B’s works speed =2x
A’s works speed = x
C’s works speed =4x
Total work=40*7x=280x
A & C complete the same work together=280x/5x=56 days - M, N & P can do a work individually in 10, 15, and 20 days respectively. If they work together then in how many days the work will be completed ?
60/1360/1455/1250/115Option A
LCM of 10,15,20=60
total work=60
M’s efficiency=60/10=6
N’s efficiency=60/15=4
P’s efficiency=60/20=3
all together can complete the total work=60/13 days - X & Y can do a work individually in 20 and 30 days respectively. X starts and works for 10 days. Then he leaves the work and remaining work completed by Y. If they got rs.600, in how much amount did A got ?
250200450300350Option D
LCM of 20 and 30=60
total work=60
X works in a day=60/20=3 works
Y works in a day=60/30=2 works
X alone work for 10 days= 3*10=30 works
remaining wrk done by Y=30/2=15 days
they got rs.600
A complete half of the work
so, A will get=600/2= rs.300 - 102 men can complete a work in 21 days, then how many men would it take to complete 17 days ?
120140126128none of theseOption C
102 men can complete a work in 21 days.
17 days work completed =102*21/17
=126 men - P can don a piece of work in 12 days and Q in 8 days. They begin together, but P goes away 3 days before the work is completed. In how many days the work will be finished ?
6825none of theseOption A
P can complete in 12 days.
Q can complete in 8 days.
Let, the total work =48
P’s efficiency =48/12 =4
Q’s efficiency =48/8 =6
Q worked for 3 days =6*3= 18 work.
P and Q worked remaining work in days =30/10 =3days.
Total work will be finished in 6 days. - A group of workers worked to finish the work in 25 days . But 10 of the total workers did not come to work and the work is finshed in 35 days. find how many workers worked in the group initially.
35382556none of theseOption A
Let
the number of workers worked initially is x.
25*x =(x-10) 35
25x= 35x-350
10x=350
x =35 - 6 men 4 boys can complete a work in 12 days . A man completes double the work than a boy. In how many days 8 men and 16 boys will complete the work.
8654none of theseOption B
Let,
A man can complete 2 work and A boy can complete 1 work.
1 man=2 boys
According to questing,
(6 men + 4 boys) can complete the work =12 days
6 men + 2 men =8 men + 8men =16 men.
1 man can do the work =(12*8)days
(8 men +16 boys) =8 men + 8 men =16 men
16 men will complete the work = 12*8/16=6 days - Avi can complete a work in 30 days. Bibhu is 20% more efficient than Avi and Pintu is 20% less efficient than Avi. In how many days the total work will be completed if they work for together.
10203040none of theseOption A
let,
efficiency of Avi ,Bibhu and Pintu be 5x, 6x, 4x respectively
total work =5x*30 = 150x
Avi, Bibhu, and Pintu will be completed total work= 150x/15x =10 days. - P can do work in 25 days and Q is 40% more efficient than P. If Q starts the work and works for 5 days and leaves the work, then in how many days the total work will be finished ?
25262423none of theseOption D
Let,
efficiency of P and Q = 5x and 7x
P can do a work in 25 days.
total work = 25*5x =125x
Q works for 5 days = 7x*5 =35x
remaining work done by P=90x/5=18 days
total work will be completed = 5+18 =23 days.
72
Quantitative Aptitude: Simplification Questions Set 114
- Direction: Find the value of ‘x’ in the following questions given below.
12^2-9^2+79= x+8^268787570none of thisOption B
144-81+79 = x+64
x = 144-81+79-64
= 78 - 1/8 of 512-35% 200+84 = x/5*30
13141516none of theseOption A
64-70+84 = 6x
6x =78
x =13 - 9871+2520+3920-x = 550
11761127611476010761none of theseOption D
16311-x = 5550
x=10761 - x^2 = √1156+32+55
14121115none of thisOption C
x^2 = 34+32+55
x = 11 - x/8*160*5*0.5 =250
6582none of theseOption B
x/8*160*5*0.5 =250
50x =250
x=5 - Direction: What will come in place of question marks (?) in the following questions below. (you are not need to calculate exact value)
299.99+529.01+320.99+625.99 =?1776188820002200none of theseOption A
300+529+321+626 =1776 - √2025.01+√3024.99-28+20-40+180=?
154160180200152Option E
45+55-28+20-40+100=152 - 550.01÷11÷5+30.10+5*15.96 = ?
120140160180none of thisOption A
550/11*5+30+80 = 10+30+80 = 120 - 39% of 2500.05+350+403 =(?)^3
14121618none of theseOption B
975+753 = (?)^3
?=12 - (?*5*20*4)/(32*120) = 30/36
1246none of thisOption A
?*5/6 =30/36
?=(30/36)*(6/5) =1
73
Quantitative Aptitude: Quadratic Equations Questions Set 76
- I. x^2+15x+56=0
II. y^2+9y+14=0x>yxx≥yx≤yx=y or no relationOption D
I. x^2+8x+7x+56=0
x=-8, -7
II. y^2+7y+2y+14=0
y=-7, -2 - I. x^2+2x-48=0
II. y^2-9y+20=0x>yxx≥yx≤yx=y or no relationOption E
I. x^2+8x-6x-48=0
x=-8, 6
II. y^2-5y-4y+20=0
y=5, 4 - I. 4x^2+16x+15=0
II. 2y^2+11y+15=0x>yxx≥yx≤yx=y or no relationOption C
I.4x^2+10x+6x+15=0
4x=-10, -6
x=-2.5, -1.5
II.2y^2+6y+5y+15=0
2y=-6, -5
y=-3, -2.5 - I. x^2-12x-108=0
II. y^2+3y-54=0x>yxx≥yx≤yx=y or no relationOption E
I. x^2-18x+6x-108=0
x=18, -6
II. y^2+9y-6y-54=0
y=-9, 6 - I. x^2-35x+306=0
II. y^2-31y+238=0x>yxx≥yx≤yx=y or no relationOption C
I. x^2-18x-17x+306=0
x=18, 17
II. y^2-17y-14y+238=0
y=17, 14 - I. 4x^2+20x+24=0
II. 5y^2+27y+10=0x>yxx≥yx≤yx=y or no relationOption E
I. 4x^2+12x+8x+24=0
4x=-12, -8
x=-3, -2
II. 5y^2+25y+2y+10=0
5y=-25, -2
y=-5, -.4 - I. x^2-10x+24=0
II. y^2-5y+6=0x>yxx≥yx≤yx=y or no relationOption A
I.x^2-6x-4x+24=0
x=6, 4
II. y^2-3y-2y+6=0
y=3, 2 - I. 2x^2+6x-20=0
II.3y^2-21+36=0x>yxx≥yx≤yx=y or no relationOption B
I. 2x^2+10x-4x-20=0
2x=-10, 4
x=-5, 2
II. 3y^2-12y-9y+36=0
3y=12, 9
y=4, 3 - I. x^2-x-132=0
II. y^2-27y+180=0x>yxx≥yx≤yx=y or no relationOption D
I. x^2-12x+11x-132=0
x= 12, -11
II. y^2-15y-12y+180=0
y=15, 12 - I. x^3=216
II. 3y^2-11y+6=0x>yxx≥yx≤yx=y or no relationOption A
I. x=6, 6
II. 3y^2-9y-2y+6=0
3y=9, 2
y=3, 2/3
74
Quantitative Aptitude: Boats and Streams Questions Set 8
- The still of boat in skill water is 7.5 km/h. If the speed of stream is 2.5 km/h, then find the time taken to go a distance of 15km and come back to starting point.
4.53453.5Option A
Speed of boat = 7.5km/h
speed of stream =2.5km/h
downstream speed of boat = 7.5+2.5 =10km/h.
Upstream speed of boat =7.5-2.5 =5km/h.
Time required =15/10+15/5 =1.5+3 =4.5 hours. - If the speed of boat in upstream and in downstream 10km/h and 20km/h respectively. Find the total distance covered by boat in still water in 6 hours .
80km.90km.80km.85km.50km.Option B
Upstream speed of boat= 10km/h.
downstream speed of boat =20km/h.
speed of boat in still water =20+10/2 =15 km/h.
Total distance covered by boat =15*6 =90 km. - The ratio of speed of boat in skill water and the current speed is 5:1 distance covered by boat in downstream speed and upstream speed is 120km. each find the speed of boat in skill water if total time taken boat in both downstream and upstream speed ids 10 hours.
2528304060Option A
Let the speed of boat in skill water= 5x
current speed =x
downstream speed of boat =5x+x =6x
upstream speed of boat =5x-x =4x
120/6x+120/4x= 10
20/x+30/x =10
x=5
speed of boat in still water =5*5 =25 km/hr - A boat along the current takes 3 hours to cover a certain distance and against the current in takes 9 hours to cover the same distance . If speed of boat in still water is 4km/h, then find the speed the current.
2311.52.5Option A
speed of boat in skill water =4km/h.
Let current speed =x
downstream speed =(4+x) km/h
upstream speed =(4-x) km/h
Let distance covered by boat =D km.
ATQ,
D/4+x =3
D =12+3x……….(1)
D /4-x =9
D =36-9x…………(2)
12+3x=36-9x
12x =24
x=2
speed of current =2 km/h. - A man’s speed with the current is 20 km/h and the speed of the current is 5km/h. Then find how much time will take by man to cover 90km in against the current.
86594Option D
downstream speed of boat =20
speed of current =5
speed of boat =20-5 =15
upstream speed of boat =15-5 =10
Time required =90/10 =9 hour. - Time taken by boat to cover 200 km in upstream is 10 hours more than the time taken by boat to cover 200 km in downstream. Total time taken by boat to cover 80 km in upstream is 8 hours. Find speed of boat in still water.
1520252410Option A
let speed of boat and current be x km/hr and y km/hr respectively
upstream speed of boat=80/8=10 km/hr
downstream =x+y
ATQ, 200/10-200/x+y=10
20-200/x+y=10
x+y=20
downstream speed of boat=20 km/hr
speed of boat in still water=20+10/2=15km/h - The upstream speed of a boat is 20% less than the downstream speed. Find speed of boat in still water if it covers 100 km in downstream and 60 km in upstream in total 7 hours.
2522.52425.528Option B
let the downstream speed=5x
upstream speed=4x
ATQ, 100/5x+60/4x=7
20/x+15/x=7
x=5
downstream speed=5*5=25
upstream speed=4x=4*5=20
boat speed=(25+20)/2=22.5 km/hr - The speed of boat in still water is 18 km/hr and current speed is 6 km/hr. If time taken by boat to cover certain distance both downstream and upstream is 12 hours. Find the distance.
10090759684Option D
speed of boat in still water=18
speed of current=6
downstream speed of boat=18+6=24
upstream speed of boat=18-6=12
let distance be D km
D/24+D/12=12
D=96 km - The sum of the speed of a boat in still water and the current is 20 km/hr. The boat takes 8 hours to cover 96 km upstream. Find the difference between the speed of boat in still water and speed of current.
1418161210Option D
let speed of boat in still water=x
current speed=20-x
upstream speed=96/8=12 km/hr
x-(20-x)=12
2x-20=12
x=16 km/hr
speed of boat in still water=16 km/hr
current speed=20-16=4 km/hr
difference=16-4=12 km/hr - A boat takes 20 hours to cover 400 km in upstream and 12 hours to cover 480 km in downstream. Speed of boat in still water is how much percent more than speed of stream ?
100%80%120%60%200%Option E
upstream speed of boat=400/20=20 km/hr
downstream speed of boat=480/12=40 km/hr
speed of boat in still water=40+20/2=30 km/hr
speed of current=40-20/2=10 km/hr
percentage=30-10/10*100=200%
75
Quantitative Aptitude: Problems on Ages Set 21
- Average age of A and B is 5 years more than the present age of C. The age of D is 3 years less than the age of C and total age of A, B, C and D is 39 years. Find the sum of age of A and B.
2628322420Option A
Let the age of C =x years
ATQ, A+B/2 =x+5
A+B =2x+10
age of D =x-3
Total age of A, B, C and D =39 years.
2x+10+x+x-3 =39
4x+7= 39
x= 8years
The sum of ages of A and B =2x+10 =26 years - Ratio of the present age of Deepak and Subham is 5:8. After 4 years ratio of their ages is 2:3, then find the age of Subham after 8 years.
4548403035Option C
Let the present age of Deepak and Subham be 5x and 8x respectively.
ATQ, 5x+4/8x+4 =2/3
16x+8 =15x+12
x=4
age of Subham after 8 years = 8x+8 =40 years. - The age of Vicky is 25% more than the age of Vikram. The age of Rashmi is 6 years more than the age of Vikram and difference between the age of Vicky and Rashmi is 2 years. What is the age of Vicky after 4 years ?
4042323544Option E
let the age of Vicky=5x
and the age of Vikram=4x
the age of Rashmi=4x+6
difference between the age of Vicky and Rashmi=2 years
5x-(4x+6)=2
5x-4x-6=2
x=8 years
Vicky after 4 years=5x+4=44 years - The average of the present age of mother and his son is 50% more than the present age of the son. If 5 years hence the sum of age of mother and his son is 70 years, then find the present age of the mother.
4048303545Option A
let the present age of mother and son be x and y years respectively
x+y/2=150/100x
x+y/2=3x/2
y=2x
also given that, x+5+2x+5=70
3x+10=70
x=20 years
present age of mother=y=2x=2*20=40 years - Average age of B and C is 20 years. The age of A is 4 years more than B and total age of A,B and C is 60 years, then find the age of A before 4 years.
2018151624Option D
average age of B and C=20 years
B+C/2=20
B+C=40
let the age of B=x
age of C=40-x
age of A=x+4
x+4+x+40-x=60
x+44=60
x=16
age of A before 4 years=x+4-2=16+4-4=16 years - Average of present age of P & Q is 24 years, average of present age of P & R is 20 years and average of present of Q & R is 16 years. Find the age of R after 8 years.
1820252824Option B
average of present age of P & Q=24
P+Q/2=24
P+Q=48
average of present age of P & R=20
P+R/2=20
P+R=40
average of present age of Q & R=16
Q+R/2=16
Q+R=32
P+Q+P+R+Q+R=48+40+32
2(P+Q+R)=120
P+Q+R=60
P+Q=48
R=60-48=12
the age of R after 8 years=12+8=20 years - Present age of son is 30% of his father age and after 5 years the ratio of age of father and son will become 5:2. What is the sum of the present age of father and son ?
4845383940Option D
let present age of father=10x
and present age of son=3x
after 5 years, 10x+5/3x+5=5/2
20x+10=15x+25
5x=15
x=3
sum=10x+3x=13x=13*3=39 years - A is 3 years older than B and after 2 years age of A will be 30 % more than that of B. Find the age of A after 5 years.
1620252428Option A
let age of B=x
and age of A=x+3
after 2 years, x+3+2=130/100(x+2)
x+5=13/10(x+2)
10x+50=13x+26
3x=24
x=8
age of A after 5 years =x+3+5=8+3+5=16 years - 5 years ago, average age of a family of 6 members was 30 years. At present one family member who is a girl got married whose age is 30 years. What is the average age of remaining 5 members of family after 4 years ?
2520242826Option B
5 years ago, average age of 6 members=30 years
at present total age of 6 members=(30*6)+(6*5)=210
one member got married who is a girl whose age is 30 years
remaining age of 5 members=180
after 4 years total age of 5 members =180+(5*4)=100
average age of 5 members after 4 years=100/5=20 years - Ratio of present age of P & Q is 4:3 and before 2 years ratio of their age is 3:2. The age of R is 12 years more than the present age of P, then find the age of R.
2520241840Option B
let present age of P & Q be 4x and 3x respectively
before 2 years, 4x-2/3x-2=3/2
8x-4=9x-6
x=2
present age pf P=4x=4*2=8
present age of R=8+12=20 years
76
Quantitative Aptitude: Mensuration Questions Set 16
- If the length of a rectangular field is increased by 15% and breadth is also increased by 10%, the area of the rectangle will be 253 m^2. What is the area of the original area of rectangle ?
400240350180200Option E
let original area of rectangle =100
percentage change in area=15+10+15*10/100=26.5
126.5=253
original area=253/126.5*100=200 m^2 - The side of square is 25% more than the length of rectangular and perimeter of square is 80cm. Ratio of length and breadth of rectangular is 4:3, then find the area of rectangular.
192215180220240Option A
let the length of rectangular=4x
side of square=5x
perimeter of square=5x*4=20x
20x=80
x=4
length of rectangular=4*4=16
ratio of length and breadth=4:3
breadth=16/4*3=12
area of rectangular=16*12=192 cm^2 - The area of square 50m^2 less than the area of a rectangular, whose breadth is 12m. If the perimeter of a square is 40m, then find the perimeter of a rectangular.
5049606570Option B
perimeter of square=40
side of square=40/4=10m
area of square=10^2=100
area of rectangular=100+50=150m^2
breadth=12m
length=150/12=12.5m
perimeter=2(12.5+12)=49 - The area of the square is in the ratio of 1444:1296. What will be the ratio of their perimeter ?
20:2119:1822:2523:2418:19Option B
The ratio of area= 1444:1296
a^2:b^2=38:36=19:18
ratio of their perimeter=19*4:18*4=19:18 - The side of square is 5cm more than the radius of a circle. The area of the circle is 154cm^2. What is the perimeter of the square ?
4464564852Option D
area of the circle=154cm^2
πr^2=154
r^2=49
r=7
side of square=7+5=12cm
perimeter of square=12*4=48cm - The length of rectangular is 18cm which is 4cm more than diameter of a circle. What is the area of the circle ?
154240150176198Option A
diameter of circle=18-4=14
2r=14
r=7
area of the circle=πr^2=22/7*7*7=154cm^2 - There is a rectangular field of 40cm in length and 30cm in breadth. On the inside of which a 5cm wide road, then find the area of road.
8005007006001000Option D
area of the outside rectangular field=40*30=1200cm^2
length of inside rectangular=40-10=30
breadth of the inside rectangular=30-10=20
area of the inside rectangular=30*20=600
the area of the road=1200-600=600cm^2 - The height and radius of a cylinder is 21cm and 12cm respectively. Find the volume of cone.
42683168436045304840Option B
height of the cylinder=21cm
radius of the cylinder=12cm
volume of the cylinder=22/7*12*12*21=22*144*3
volume of the cone=1/3*volume of cylinder
=1/3*22*144*3=3168cm^2 - The ratio of the length of the diagonals of a rhombus is 4:3. If the perimeter of the rhombus is 160m. What is the length of the diagonal of a square whose area is same as that of rhombus ?
15√316√320√225√524√2Option B
let the diagonals of the rhombus be 4x and 3x
side length of the rhombus=√(4x)^2+(3x)^2
=√16x^2+9x^2
=25x^2=5x
perimeter=4*5x=20x=160
20x=160
x=8
two diagonal of the rhombus=32 and 24
area=1/2*32*24=384
let the diagonal of the square=D
side of the square=D/√2
(D/√2)^2=384
D^2/2=384
D=16√3 - The circumference of the circle is 176cm and the radius of circle is 4 less than side of the square. Find the area of the square.
576100078410241444Option D
2πr=176
r=176*7/44=28
side of square=28+4=32
area of square=32*32=1024
77
Quantitative Aptitude: Simplification Questions Set 113
- Directions: What will come in place of questions (?) marks in the following given below questions?
3030*8/15-1500÷ 6+1000=?24082505320034182366Option E
202*8-1500/6+1000=?
1616-250+1000=2366 - 52*45+32*12-45*80=?
-876-875-976-850-880Option A
2340+384-3600
2724-3600=-876 - 60% of 180+1331÷ 11+48=?
278277375477240Option B
108+121+48=277 - √196*25*4+1800÷ 60+30=?
240200340180250Option B
14*5*2+30+30=?
140+60=200 - 2 5/3+8 4/6+ 5 4/6- 7 2/3 =?
8 11/36 12/55 9/1010 7/88 4/11Option A
2+8+5-7 (10+4+4+4/6)
= 8 (22/6) =8 11/3 - Directions: What will come in place of questions (?) marks in the following given below questions ? (you are not calculate exact value)
∛1728.04+ √2304.02 + √2024.86= ?105108110210420Option A
12+48+45 =105 - 1350.04*8/45+366*4-10% of 899.99 =?
15201614164028452840Option B
1350*8/45+366*4-10% of 900
=240+1464-90 =1704-90
=1614 - 240% of 600.05 +45.88*10 -40% of 499.99= ?
800820450804480Option D
144+460+200 =804 - 12.5% of 800 + 48.05*2 – √1295.96
170180200160100Option D
1/8*800 + 96 -36
=100+60 =160 - 4400+3815.99 + 5600.04 +6449.96 =?
1814020266241602046616266Option B
4400 + 3816 + 5600 +6450 =20266
78
Quantitative Aptitude: Time and Work Set 27
- A, B and C alone can do a work in 8 days , 12 days and 6 days respectively. Find how many days they take together to complete work ?
6 days8 days2 2/3 days4 days3 daysOption C
LCM of 8 , 12 and 6 = 24
total work = 24
efficiency of A = 24/8 = 3
efficiency of B = 24/12 = 2
efficiency of C = 24/6 = 4
time taken = 24/9 = 2 2/3 days - P and Q alone can do a work in 30 days and 20 days respectively. P works for 15 days and left the work, remaining work done by B. Find how many days required to complete the remaining work ?
10 days8 days20 days18 days16 daysOption A
LCM of 30 and 20 = 60
total work = 60
efficiency of P = 60/30 = 2
efficiency of Q = 60/20 = 3
P completed work in 15 days = 15 * 2 = 30
time taken by Q to complete remaining work = 60 – 30 /3 = 10 days - A can complete 40% of work in 8 hours and while B alone can do the same work in 24 hours. Find the time taken by A and B together to complete the 60% of the work ?
5 2/3 days8 3/5 days4 days6 6/11 days8 daysOption D
A alone can do all work = 8/40 * 100 = 20 days
LCM of 20 and 24 = 120
efficiency of A = 120/20 = 6
efficiency of B = 120/24 = 5
time taken by A and B together to complete 60% of the work = 120/11 * 60/100 = 6 6/11 days - A and B alone can do a piece of work in 12 hours and 15 hours respectively. If they do the work alternatively for 1 hours each starting with A, then find how many hours will the work be completed ?
5 hours3 hours8 1/5 hours12 1/4 hours13 1/4 hoursOption E
LCM of 12 and 15 = 60
total work = 60
efficiency of A = 60/12 = 5
efficiency of B = 60/15 = 4
work completed in 2 hours = 5 + 4 = 9 works
(2 * 6) hours = (9 * 6) work
12 hours = 54 works
A works in another hours = 5 work
remaining 1 work completed by B = 14 hours
total time = 12 + 1 + 1/4 = 13 1/4 hours - A, B and C alone can do a piece of work in 3 days. If A alone can do in 6 days and C alone can do it in 18 days, how long will B alone take to complete the work ?
8 days9 days18 days6 days4 daysOption B
LCM of 3, 6 and 18 = 18
total work = 18
efficiency of A, B and C = 18/3 = 6
efficiency of A = 18/6 = 3
efficiency of C = 18/18 = 1
efficiency of B = 6 – ( 3 + 1 ) = 2
B alone can do the work = 18/2 = 9 days - P and Q undertook to do a piece of work for rs.3500. P alone can do it in 12 days and Q alone in 20 days. If they finished the work with the help of R in 6 days. What is share of R ?
800700850650725Option B
LCM of 12, 20 and 6 = 60
efficiency of P = 60/12 = 5
efficiency of Q = 60/20 = 3
efficiency of P, Q and R = 60/6 = 10
efficiency of R = 10 – ( 5 + 3 ) = 2
share of R = 3500 * 2 / 10 = 700 - Rita and Gita can do a piece of work individually in 40 days and 60 days respectively. If they work on alternate days starting with Gita, then in how many days will the work get finished ?
28 days24 days17 days48 days46 daysOption D
LCM of 40 and 60 = 120
efficiency of Rita = 120/40 = 3
efficiency of Gita = 120/60 = 2
starting with Gita work completed in 2 days = 5
time required to complete total work = 24 * 2 = 48 days - A and B can do a work in 12 days. B and C can do the same work in 20 days. A and C can also do the same work in 30 days. If they all work together in how many days will they complete the work ?
10 days14 days12 days13 days15 daysOption C
LCM of 12, 20 and 30 = 120
efficiency of A and B = 120/12 = 10
efficiency of B and C = 120/20 = 6
efficiency of A and C = 120/30 = 4
A + B + B + C + A + C = 10 + 6 + 4 = 20
2(A + B + C) = 20
A + B + C = 10
time 120/10 = 12 days - 8 men or 12 women can finish a work in 25 days. How many days will 6 men ad 11 women can finish the same work ?
15 days14 days28 days30 days32 daysOption A
8 men = 12 women
men/women = 12/8 = 3/2
total work = 8 * 3 * 25 = 600
time required = 600 /(6 * 3 + 11 * 2) = 600/40 = 15 days - A, B and C can complete a job in 9 days, 10 days and 15 days respectively. A, B and C start the work together and after 2 days B and C leave the work. Find how many days taken by A to complete the remaining work ?
6 days18 days14 days4 days8 daysOption D
LCM of 9, 10 and 15 = 90
efficiency of A = 90/9 = 10
efficiency of B = 90/10 = 9
efficiency of C = 90/15 = 6
A, B and C complete work in 2 days = 2(10 + 9 + 6) = 50
remaining work = 90 – 50 = 40
time taken by A to complete remaining work = 40/10 = 4 days
79
Quantitative Aptitude: Data Interpretation Questions Set 154
Direction: Given below the table shows the total number of books shopkeeper and also given that the ratio of Math and English book sold by each shopkeeper.
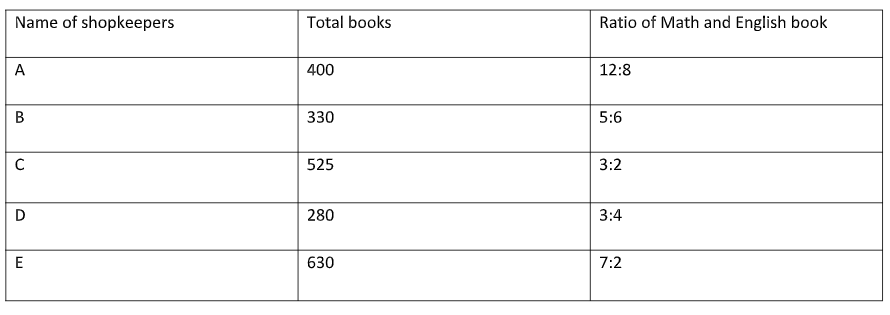
- Total number of math book sold by A and C together is how much more/less then total number of English book sold by C and D together .
285185100120none of theseOption B
Math book sold by A =400*12/20=240
Math book sold by B =525*3/5 =315
English book sold by C =525*2/5 =210
English book sold by D =280*4/7 =160
Difference =(240+315)-(210+160)
=555-370 =185 - What is the ratio of English book sold by B to math book sold by E.
49:1818:4920:2012:14none of theseOption B
English book sold by B = 330*6/11=180
Math book sold E = 630*7/9 =490
Ratio =180:490 =18:49 - Find the average numbers total of books sold by B and E together.
400490300480none of theseOption D
(330+630)/2 =960/2 =480 - Total number of math books sold by C and B together is what present more/less than total numbers of English book sold by shopkeeper A and E together.
40%50%60%55%none of theseOption D
math book sold by C =525*3/5=315
math book sold by B =330*5/11=150
English book sold by A = 400*8/20=160
English book sold by E =630*2/9=140
present more =(465-300)/300*100=55% - Find the total English sold by shopkeeper D and E together .
200300350220none of theseOption B
English book sold by D =280*4/7
English book sold by E =630*2/9=140
total=160+140=300 -
Direction: Given below the pie-chart shows percentage distribution of mobile mobile produced by different company. Study the following pie-chart and solve the following questions given below.
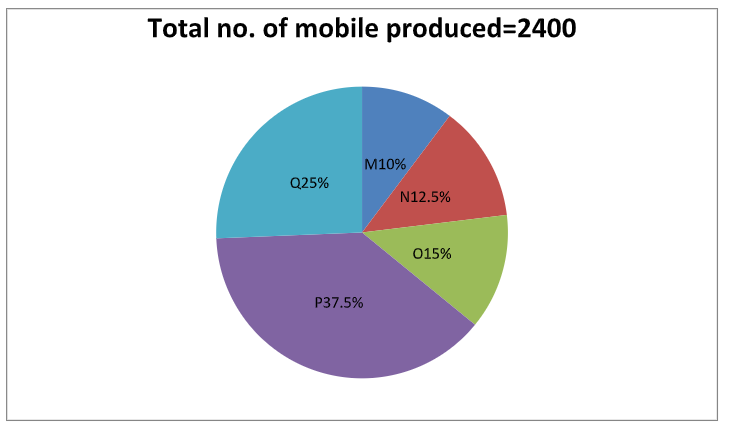
Total no. of mobile produced by company O is what percent of total no. of mobile produced by company M.16015012010080Option B
15/10*100=150% - Find the ratio of no. of mobile produced by company Q and M together to company P and O together .
2:34:56:88:4none of theseOption A
No. of mobile produced by Q =240*25/100 =600
No. of mobile produced by M =240*10/100 =240
No. of mobile produced by P=240*3/8 =900
No. of mobile produced by O=240*15/100 =360
Ratio =(600+240):(900+360)=840:1260= 2:3 - What is the average no. of mobile produced by M, O, Q together ?
280420520400440Option D
Average no. mobile produced by M,O and Q =(10+15+25)/3%
=50/300*2400=400
- Find the difference between total no. of mobile produced by O and Q together how much percent more/less total no. of mobile produced by P and N together.
20%, more20%, less10%, less25%, more15%, moreOption B
P and N together=50%
O and Q together=40%
percent less=(50-40)/50*100=20% - Find the difference between total no. of mobile produced by M and N together to no. of mobile produced by O.
180200240300160Option A
No. of mobile produced by M=2400*10/100=240
No. of mobile produced by N=2400*1/8=300
No. of mobile produced by O=2400/*15/100=360
Difference=(240+300)-360=180
80
Quantitative Aptitude: Probability Questions – Set 21
- If coins are tossed, then find the probability of getting at least 3 tails on the face.
8/941/41/22/5Option D
Required = (5C3) + (5C4) + (5C5) = 10 + 5 + 1 = 16
total = 2^5 = 32
probability = 16/32 = 1/2 - A bag contains 4 red balls, 2 black balls and 5 yellow balls. 3 balls are drawn randomly, find the probability of getting all balls are of red balls.
2/651/54/1655/82/165Option C
Required = 4C3 = 4
total = 11C3 = 165
probability = 4/165 - A box contains 4 white balls and 8 blue balls. 2 balls are drawn randomly from the box in succession without replacement. What is the probability that they are different colors ?
6/175/1218/2516/331/8Option D
Probability = 4/12 * 8/11 * 4/11 * 8/12 = 2 * 4/12 * 8/11 = 16/33 - If 2 cards are selected randomly from a pack of 52 card, then what is the probability that all are face cards ?
11/2218/254/2258/292/441Option A
Probability = (12C2) / (52C2)
= 12 * 11 / 52 * 51 = 11/221 - Five men and 4 women sit in a row for eating food. What is the probability that they will sit in alternate position ?
1/262/853/821/1262/ 85Option D
Probability = 5! * 4! / 9! = 1/126 - What is the probability that number selected from number 1, 2 , 3 … 100 is a prime number ?
2/51/45/81/24/7Option B
Probability = 25/100 = 1/4 - In how many different ways can the letters of the word “SHARE” be arranged ?
260150160120140Option D
Number of ways = 5! = 120 - One bag contains 4 blue balls and 3 green balls. Another bag contains 5 red balls and 7 blue balls. If one ball is drawn randomly from each bag then, what is the probability that both are blue balls ?
2601/81/34/17Option D
Probability = (4C1) / (7C1) * (7C1) / (12C1) = 1/3 - A box contains 4 green balls , 2 white balls and 4 blue balls. If three balls are drawn together from the box, then what is the probability of selecting that these three balls are the same colors ?
8/1717/182/251/151/30Option D
Probability = (4C3) / (10C3) + (4C3) / (10C3)
= 1/30 + 1/30 = 1/15 - How many words can be formed with the help of the letters of the word “SCHOOL” in such a way that all the words start with ‘L’ ?
4060428570Option B
Number of ways = 5!/2! = 120/2 = 60
81
Quantitative Aptitude: Time and Work Set 26
- A, B and C alone can do a work in 8 days , 12 days and 6 days respectively. Find how many days they take together to complete work ?
6 days8 days2 2/3 days4 days3 daysOption C
LCM of 8 , 12 and 6 = 24
total work = 24
efficiency of A = 24/8 = 3
efficiency of B = 24/12 = 2
efficiency of C = 24/6 = 4
time taken = 24/9 = 2 2/3 days - P and Q alone can do a work in 30 days and 20 days respectively. P works for 15 days and left the work, remaining work done by B. Find how many days required to complete the remaining work ?
10 days8 days20 days18 days16 daysOption A
LCM of 30 and 20 = 60
total work = 60
efficiency of P = 60/30 = 2
efficiency of Q = 60/20 = 3
P completed work in 15 days = 15 * 2 = 30
time taken by Q to complete remaining work = 60 – 30 /3 = 10 days - A can complete 40% of work in 8 hours and while B alone can do the same work in 24 hours. Find the time taken by A and B together to complete the 60% of the work ?
5 2/3 days8 3/5 days4 days6 6/11 days8 daysOption D
A alone can do all work = 8/40 * 100 = 20 days
LCM of 20 and 24 = 120
efficiency of A = 120/20 = 6
efficiency of B = 120/24 = 5
time taken by A and B together to complete 60% of the work = 120/11 * 60/100 = 6 6/11 days - A and B alone can do a piece of work in 12 hours and 15 hours respectively. If they do the work alternatively for 1 hours each starting with A, then find how many hours will the work be completed ?
5 hours3 hours8 1/5 hours12 1/4 hours13 1/4 hoursOption E
LCM of 12 and 15 = 60
total work = 60
efficiency of A = 60/12 = 5
efficiency of B = 60/15 = 4
work completed in 2 hours = 5 + 4 = 9 works
(2 * 6) hours = (9 * 6) work
12 hours = 54 works
A works in another hours = 5 work
remaining 1 work completed by B = 14 hours
total time = 12 + 1 + 1/4 = 13 1/4 hours - A, B and C alone can do a piece of work in 3 days. If A alone can do in 6 days and C alone can do it in 18 days, how long will B alone take to complete the work ?
8 days9 days18 days6 days4 daysOption B
LCM of 3, 6 and 18 = 18
total work = 18
efficiency of A, B and C = 18/3 = 6
efficiency of A = 18/6 = 3
efficiency of C = 18/18 = 1
efficiency of B = 6 – ( 3 + 1 ) = 2
B alone can do the work = 18/2 = 9 days - P and Q undertook to do a piece of work for rs.3500. P alone can do it in 12 days and Q alone in 20 days. If they finished the work with the help of R in 6 days. What is share of R ?
800700850650725Option B
LCM of 12, 20 and 6 = 60
efficiency of P = 60/12 = 5
efficiency of Q = 60/20 = 3
efficiency of P, Q and R = 60/6 = 10
efficiency of R = 10 – ( 5 + 3 ) = 2
share of R = 3500 * 2 / 10 = 700 - Rita and Gita can do a piece of work individually in 40 days and 60 days respectively. If they work on alternate days starting with Gita, then in how many days will the work get finished ?
28 days24 days17 days48 days46 daysOption D
LCM of 40 and 60 = 120
efficiency of Rita = 120/40 = 3
efficiency of Gita = 120/60 = 2
starting with Gita work completed in 2 days = 5
time required to complete total work = 24 * 2 = 48 days - A and B can do a work in 12 days. B and C can do the same work in 20 days. A and C can also do the same work in 30 days. If they all work together in how many days will they complete the work ?
10 days14 days12 days13 days15 daysOption C
LCM of 12, 20 and 30 = 120
efficiency of A and B = 120/12 = 10
efficiency of B and C = 120/20 = 6
efficiency of A and C = 120/30 = 4
A + B + B + C + A + C = 10 + 6 + 4 = 20
2(A + B + C) = 20
A + B + C = 10
time 120/10 = 12 days - 8 men or 12 women can finish a work in 25 days. How many days will 6 men ad 11 women can finish the same work ?
15 days14 days28 days30 days32 daysOption A
8 men = 12 women
men/women = 12/8 = 3/2
total work = 8 * 3 * 25 = 600
time required = 600 /(6 * 3 + 11 * 2) = 600/40 = 15 days - A, B and C can complete a job in 9 days, 10 days and 15 days respectively. A, B and C start the work together and after 2 days B and C leave the work. Find how many days taken by A to complete the remaining work ?
6 days18 days14 days4 days8 daysOption D
LCM of 9, 10 and 15 = 90
efficiency of A = 90/9 = 10
efficiency of B = 90/10 = 9
efficiency of C = 90/15 = 6
A, B and C complete work in 2 days = 2(10 + 9 + 6) = 50
remaining work = 90 – 50 = 40
time taken by A to complete remaining work = 40/10 = 4 days
82
Partnership Questions Quantitative Aptitude: Partnership Set 22
- A started a business with an initial investment of rs.4200 and after 5 months B and c joined the business investing rs.5400 and rs.6000 respectively. If total profit of the business at the end of the year is rs.15500 , then find the profit share of B ?
48003750284045004450Option D
Profit sharing ration of A , b and C = (4200 *12) : (5400 * 7) : (6000 * 7) = 12 : 9 : 10
total profit = 15500
profit share of B = 15500 * 9/31 = 4500 - The investment ratio of A , B and C in a business is 4 :3 :7. If they invested their capital for 7 months , 8 months and 6 months respectively , then in which ratio they distributed their profit at the end of the year ?
5 : 3 : 26 : 4 :35 : 2 : 32 : 3 : 814 : 12 : 21Option E
Profit sharing ratio of A, B and C = (4 * 7) : (3 * 8) : (7 * 6) = 14 : 12 : 21 - A , B and C started a business. a receives 3/5 of the profit and the remaining profit shared by B and C equally. If difference between profit of A and B is rs.500, then what is total profit of the business ?
3450140020001250600Option D
Let total profit of the business = 5x
profit share of A = 5x * 3/5 = 3x
remaining profit = 2x
profit share of B and C = x and x respectively
3x – x = 500
x = 250
total profit of the business = 5x = 5 * 250 = 1250 - Three partners A , B and C started a business with investing rs.4000, rs.6500 and rs.5500 respectively. After 2 years A invested rs.2500 more , B withdraws rs.1500 and C invests rs.500 more in the business. Total profit of the business at the end of the three years rs.19800, then find the profit share of A ?
48505800354048005800Option E
Profit sharing ratio of A , B and C = (4000 * 2 + 6500 * 1) : (6500 * 2 + 5000 * 1) : (5500 * 2 + 6000 * 1)
= 29 : 36 : 34
profit share of A = 19800 * 29/99 = 5800 - A , B and C enter into a partnership farm. Profit share of A and B rs.1200 ad rs.1800 respectively out of the total profit of rs.4500. If investment made by A rs.25000, then ho much amount invested by C in the business ?
2550028000400003125045000Option D
Total profit = 4500
total profit of A and B = 1200 + 1800 = 3000
profit share of C = 4500 – 3000 = 1500
investment = of c = 25000/1200 * 1500 = 31250 - A and B started a business with capitals of rs.45000 and rs.40000 respectively. After 4 months A withdraws from the business. At the end of a year they got rs. 7700 as total profit. Find the share of A ?
28002100440055003800Option B
Profit sharing ratio of A , B = (45000 * 4) : (40000 * 12) = 3 :8
profit share of A = 7700 * 3/11 = 2100 - Ram , Hari and Shiva started a business with total capital of rs.15000. Hari invests rs.1600 less than Ram and Shiva invests rs.3200 more than Hari. If total profit at the end of a year is rs.4500, then how much profit Shiva gets ?
22403450152019802480Option D
Let Ram invests = rs.x
Hari invests = x – 1600
Shiva invests = x – 1600 + x +3200
total profit = 15000
x + x – 1600 + x + 600 = 15000
Ram invests = 5000
Hari invests = 5000 – 1600 = 3400
Shiva invests = 3400 + 3200 = 6600
their profit sharing ratio = 5000 : 3400 : 6600
profit share of Shiva = 4500 * 33/75 = 1980 - A and B started a business with capitals of rs.2500 and rs.3000. A got 20% the profit for maintaining the business and the rest distributed in their 744 in all . what is the profit share of B ?
840530520576790Option D
Profit sharing ratio of A , B = 2500 : 3000 = 5 : 6
let total profit = 110x
A get 20% of the profit = 10x * 20/100 = 22x
remaining profit = 110x – 22x = 88x
profit share of A = 88x
profit share of A = 88x * 5/11 = 40x
profit share of B = 88x * 6 / 11 = 48x
A got in all = 744
62x = 744
x = 12
profit share of B = 48 * 12 = 576 - Total capital invested by P , Q, R and S in the business is rs.41600. At the end of the year the shares of their profit are rs.400 , rs, 600 , rs240 rs.840 respectively. What is the capital invested by R ?
54005800320048005320Option D
Profit sharing ratio of P, Q, R and S = 400 : 600 : 240 : 840
= 10 : 15 : 6 : 21
investment by R 41600 * 6/52 = 4800 - A, B and C started a partnership business rs. 8400 , rs 5000 and rs.6200 respectively. If they invested their capital for 5 months , 6 months and 8 months , how much profit B gets at the end of the year ?
480520380can’t determined.350Option D
Here , profit is not given so, we can’t calculate profit share of B.
83
Quantitative Aptitude: Simplification Questions Set 112
- Directions : What should come in place of questions marks ( ? ) in the following questions ?
√1296 + √2025 – √2916 = ?2527373618Option B
36 + 45 – 54 = ?
? = 27 - 45% of 830 + 22% 740 – 148 = ?
463.5825.6388.3540332.4Option C
373.5 + 162.8 – 148 = ?
? = 388.3 - (18)^2 + (52)^2 – 140 + 245 = ?
25203240282429233048Option D
324 + 2704 – 105 = ?
? = 2923 - 7862 – 2136 + 5625 – 6524 = ?
53283428362524504827Option E
13487 – 8660 = ?
? = 4827 - 25% of 480 + 24% of 420 – 8^2 = ?
520324219319450Option C
120 + 100.8 – 64 + 62.2 = ?
? = 283 – 64
? = 219 - 23% of 1200 + 11.11% of 729 + 375 = ?
520732632534420Option B
276 + 81 + 375 = ?
? = 732 - 1/9 of 3/5 of 375 + 185 = ?
320260420440360Option B
1/9 * 3/5 * 375 + 235 = ?
25 + 235 = ?
? = 260 - 520 + 389 – (13)^2 + (15)^2 = ?
965845320740670Option A
520 + 389 + 225 – 169 = ?
? = 1134 – 169
? = 965 - 20% of 540 + 24% of 1200 – √1728 = ?
285384280320296Option B
108 + 288 – 12 = ?
? = 396 – 12
? = 384 - 640/20 – 180 + 324 – 20 = ?
120156124320450Option B
32 + 324 – 180 – 20 = ?
? = 356 – 200
? = 156
84
Quantitative Aptitude: Ratio and Proportion Questions Set 11
- Vessels A and B contain the mixture of alcohol and water in the ratio of 4 : 5 and 3 : 2 respectively. If vessels A and B are mixed then what is the ratio of new mixture which is obtained ?
5 : 835 : 2947 : 435 : 22 : 5Option C
Quantity of alcohol and water in vessel B = 3/5 and 2/5
New ratio = (4/9 + 3/5) : (5/9 + 2/5)
= (20 + 27/45) : (25 + 18/45)
= 47 : 43 - The ratio of total students to number girl of a particular class is 8 : 5. If numbers of boys of that class is 450 , then find the total number of students.
12201100120013451000Option C
Let total number of students = 8x
number of girls = 5x
number of boys = 8x – 5x = 3x
3x = 450
x = 150
Total students = 1200 - Sipun has three types of coins 10 paisa, 50 paisa and 20 paisa of coin is 4 : 2 : 5. If total coins worth is rs.96, then find the number of 50 paisa coins.
6075488040Option D
Let number of 10 paisa, 50 paisa and 20 paisa coins are 4x, 2x and 5x respectively.
4x * 10 + 2x * 50 + 5x * 20 = 9600
40x + 100x + 100x = 9600
x = 40
number of 50 paisa coins = 2x = 80 - The ratio of monthly income of A and B is 3 : 5 and the ratio of the expenditure of A and B is 6 : 11. If the savings of A and B are rs.6000 and rs.8000 respectively. What is expenditure of B ?
4800042000430003500030000Option E
Let income of A and B are 3x and 5x.
3x – 6000/5x – 8000 = 6/11
33x – 66000 = 30x – 48000
3x = 18000
x = 6000
income of B = 5 * 6000 = 30000 - There are total of 48 employees in a company. The ratio of male employees to the female employees is 5 : 3. How many more female employees to be recruited to that the ratio becomes 1 : 1 ?
1015122025Option C
Number of male employees = 48 * 5/8 = 30
number of female employees = 48 * 3/8 = 18
Let number female employees recruited = x
30/18 +x = 1/1
18 + x = 30
x = 12 - The ratio of milk and water in a mixture is 6 : 5 and 22 liter of mixture is replaced with water, so that ratio of milk and water in new mixture is 3 : 8, then how much quality of water in the mixture initially ?
20 liters32 liters28 liters35 liters40 litersOption A
Let quality of milk and water are 6x and 5x respectively.
(6x – 22 * 6/11)/(5x – 22 * 5/11+22)= 3/8
6x – 12/5x + 12 = 3/8
48x – 96 = 15x + 36
33x = 132
x = 4
quality of water initially = 5x = 5 * 4 = 20 liters. - The ratio of income to expenditure of A is 4 : 3 and that of B 5 : 3. If savings of B is double that of A, then what could be the ratio of total income of A and B together to the total expenditure of A and B together ?
2 : 34 : 53 : 25 : 86 : 9Option C
Let income and expenditure of A = 4x and 3x
income and expenditure of B = 5x and 3x
saving of A = 4x – 3x = x
saving of B = 5x – 3x = 2x
ratio = (4x + 5x) : (3x + 3x)
= 9x : 6x = 3 : 2 - The ratio of male employees to female employees of a bank is 5 : 4. If 10 male employees left the job and 4 more female employees joined the bank, so that ratio between male to female employees is 7 : 8, then find the total employees of the bank initially ?
8581927848Option B
Let male and female employees are 5x and 4x respectively.
5x – 10/4x + 4 = 7/8
40x – 80 = 28x + 28
12x = 108
x = 9
total male and female employees initially = 5x + 4x = 9x = 9 * 9 = 81 - The seats for commerce, science and arts in a college are in the ratio of 5 : 4 : 8. If these seats are increased by 20%, 50% and 75% respectively, what will be the ratio of the increased seats of the college ?
5 : 2 : 86 : 2 : 35 : 4 : 86 : 6 : 144 : 3 : 2Option D
Let commerce seats = 5x
science seats = 4x
Arts seats = 8x
ratio of commerce, science and arts seats after increased = (5x * 6/5) : (4x * 3/2) : (8x * 7/4)
= 6x : 6x : 14x
= 6 : 6 : 14 - Total income of A, B and C is rs.9400. If A’s income is 4/5th of B’s income and B’s income is 3/4th of C’s income, then find the income of C.
34004000520032002800Option B
A = 4/5 B
A/B = 4/5
A/B = 4 * 3/5 * 3 = 12/15
B = 3/4 *C
B/C = 3/4
B/C = 3 * 5/4 * 5
B/C = 15/20
ratio of A, B and C = 12 : 15 : 20
B’s income = 9400 * 20/47 = 4000
85
Quantitative Aptitude: Number Series Set 151
- Directions : what should come in place of questions (?) marks in the following number series ?
18, 37, 56, ?, 947260807574Option D
The series is, +19, +19, +19… - 15, 8, 9, 20, ?, 256
6840429263Option E
The series is, (*.5 + 5), (*1 + 1), (*2 + 2), (*3 + 3), (*4 + 4) - 1448, 936, 593, 377, ?, 188
354252192264260Option B
The series is, -8^3, -7^3, -6^3, -5^3, -4^3 - 23, 18, 25, 14, 27, 10, ?
302563229Option E
The series is , +2, -4, +2, -4 of alternate numbers. - 34, 53, 76, 105, ?, 169
136125140142148Option A
The series is, +19, +23, +29… ( additions of prime numbers ) - Directions : What will be the wrong number in the given wrong number series ?
17, 33, 69, 133, 233, 3546913317233354Option E
The series is, +4^2, +6^2, +8^2, +10^2, +12^2 - 4, 10, 22, 42, 72, 120
1202242472Option A
The series is, +(2^2 + 2), +(3^2 + 3), +(4^2 + 4), +(5^2 + 5), +(6^2 + 6) - 45, 83, 128, 215, 339, 550
21533912855083Option A
The series is (45 + 83), (83 + 128), (128 + 211), (211 + 339) - 32, 64, 192, 768, 3846, 23040
1923264384623040Option D
The series is *2, *3, *4, *5, *6 - 28, 34, 46, 70, 118, 220
462202811846Option B
The series is (+6), (+12), (+24), (+48), (+96)
86
Quantitative Aptitude: Problems on Ages Set 20
- The present age of A and B are 29 and 32 years respectively, after how many years ratio of ages of B and A becomes 14 : 13 ?
5 years8 years12 years10 years14 yearsOption D
Let after x years ratio of ages of A and B becomes 13 : 14
29 + x/32 + x = 13/14
x = 10 years. - The ratio of present ages of A and B is 3 : 2 and ratio of present ages of C and B is 5 : 4. If total present age of A, B and C is 120 years then, what the age of B before 6 years.
2818322926Option E
Ratio of age A and B = 3 : 2
ratio of B and C = 4 : 5
A : B : C = 6 : 4 : 5
Let total ages of A, B and C = 15x
15x = 120
x = 8
present age of B = 8 * 4 = 32 years.
before 5 years age of B = 32 – 5 = 26 years. - The ratio of present age of Papu and Sipu is 4 : 5. The ratio of age of Papu after 4 years and Sipu before 8 years is 9 : 8, then find the age of Papu after 14 years.
45 years35 years28 years46 years52 yearsOption D
Let present age of Papu and Sipu are 4x and 5x respectively.
4x + 4/5x – 8 = 9/8
45x – 72 = 32x + 32
13x = 104
x = 8
the age of Papu after 14 years = 4x + 14 = 46 years - The present age of father is two times more than the present age of son. If after 6 years the ratio of age of father and son is 7 : 3, then find the age of son after 5 years.
1518172028Option C
Let present age of son = x
present age of father = 3x
3x + 6/ x + 6 = 7/3
9x + 18 = 7x + 42
x = 12
age of son after 5 years = 12 + 5 = 17 years. - The age of brother is four times of his sister and after 18 years the ratio of age of brother and sister is 2 : 1. What is age of brother after 4 years ?
2028464052Option D
Let the age of sister = x
the age of brother = 4x
4x + 18/x + 18 = 2/1
4x + 18 = 2x + 36
2x = 18
x = 9
The age of brother after 4 years = 4x + 4 = 40 years. - A is as much younger to B as he is elder to C and the sum of the age of B and C is 52 years, then what is the age of A ?
1417282326Option E
Total age of B and C = 52
B – A = A – C
2A = B + C
2A = 52
A = 26 years. - The ratio of the present age of A and B is 8 : 5. If the A’s present age is 5 years more than B’s age after 10 years, then what is the sum of age A and B after 5 years ?
8075606482Option B
Let present age of A and B are 8x and 5x respectively.
8x – (5x + 10) = 5
8x – 5x – 10 = 5
3x = 15
x = 5
age of A after 5 years = 8x + 5 = 45
age of B after 5 years = 5x + 5 = 30
sum = 45 + 30 = 75 years. - The ratio between the present ages of A and B is 5 : 6. If the ratio between the one – third age of A and half that of B is 5 : 9, then what is the present age of A ?
45386254can not determined.Option E
Let the present age of A and B are 5x and 6x respectively.
(5x/3)/(6x/2) = 5/9
5x/3 * 9 = 6x/2 * 5
Here, we can not calculate the present age of A. - Two years ago, the age of mother was four times as old as her daughter. After four years, difference between the age of mother and the age of daughter is 18 years. Find the age of mother after 8 years.
3834425648Option B
Two years ago let age of daughter = x
age of mother = 4x
present age of mother and daughter = (4x + 2), (x + 2)
After 4 years, the age of mother = 4x + 2 + 4 = 4x + 6
the age of daughter = x + 2 + 4 = x + 6
difference = 20
4x + 6 – (x + 6) = 18
4x + 6 – x – 6 = 18
3x = 18
x = 6
the age of mother after 8 years = 4x + 2 + 8 = 24 + 10 = 34 years. - The ratio between the present ages of P and Q is 4 : 5. If the ratio between their ages 4 years hence, becomes 14 : 17. What is Q’s age of present ?
4530325726Option B
Let present age of P and Q are 4x and 5x respectively.
4x + 4/5x + 4 = 14/17
70x + 56 = 68x + 68
2x = 12
x = 6
Q’s present age = 5x = 30 years.
87
Quantitative Aptitude: Quadratic Equations Questions Set 75
- I. x^2 – 8x + 12 = 0
II. 2y^2 + 7y + 5 = 0X ≥ YX ≤ YX > YX < YX= Y or no relation.Option C
I. x^2 – 6x – 2x + 12 = 0
x = 6, 2
II. 2y^2 + 5y + 2y + 5 = 0
2y = -5, -2
y = -2.5, -1 - I. y^2 = 196
II. x^2 – 30x + 225 = 0X ≥ YX > YX ≤ YX= Y or no relation.X < YOption B
I. y = 14, -14
II. x^2 – 15x – 15x + 225 = 0
x = 15, 15 - I. 4x^2 + 14x – 8 = 0
II. y^2 + 8y + 16 = 0X ≤ YX= Y or no relation.X < YX > YX ≥ YOption E
I. 4x^2 + 16x – 2x – 8 = 0
4x = -16, 2
x = -4, .5
II. y^2 + 4y + 4y + 16 = 0
y = -4, -4 - I. x^3 = 1728
II. y^2 – 24y + 144 = 0X < YX ≤ YX= Y or no relation.X ≥ YX > YOption C
I. x = 12
II. y^2 – 12y – 12y + 144 = 0
y = 12, 12 - I. x^2 – 32x + 156 = 0
II. y^2 – 33y + 140 = 0X ≥ YX > YX ≤ YX= Y or no relation.X < YOption D
I. x^2 – 26x – 6x + 156 = 0
x = 26, 6
II. y^2 – 28y – 5y + 140 = 0
y = 28, 5 - I. 2x^2 – 24x + 64 = 0
II. y^3 = 512X < YX= Y or no relation.X ≤ YX > YX ≥ YOption C
I. 2x^2 – 16x – 8x + 64 = 0
2x = 16, 8
x = 8, 4
II. y^3 = 512
y = 8 - I. x^2 = 400
II. y = √400X ≥ YX < YX ≤ YX= Y or no relation.X > YOption C
I. x^2 = 400
x = 20, -20
II. y = √400
y = 20 - I. x^2 – 7x + 12 = 0
II. y^2 + 5y + 6 = 0X ≤ YX < YX= Y or no relation.X > YX ≥ YOption D
I. x^2 – 4x – 3x + 12 = 0
x = 4, 3
II. y^2 + 3y + 2y + 6 = 0
y = -3, -2 - I. x^2 – 14x + 48 = 0
II. y^2 = 64X > YX < YX ≥ YX ≤ YX= Y or no relation.Option E
I. x^2 – 8x – 6x + 48 = 0
x = 8, 6
II. y^2 = 64
y = + 8, – 8 - I. 2x^2 + 19x + 34 = 0
II. y – 8y + 15 = 0X < YX > YX ≤ YX ≥ YX= Y or no relation.Option A
I. 2x^2 + 17x + 2x + 3 = 0
2x = – 17, – 2
x = – 8.5, – 1
II. y – 5y – 3y + 15 = 0
y = 5, 3
88
Quantitative Aptitude: Profit and Loss Set 28
- A person sold an article earned a profit of rs.2500 after giving a discount of 25%. If he had sold it for rs.500 more he would have earned a profit of 60%, then what is the cost price of the article ?
65006000550075005000Option E
Let MP of an article = 4x
SP of an article = 4x – x = 3x
profit = 2500
CP = 3x – 2500
If he sold it rs.500 more,
3x + 500 = (3x – 2500)8/5
15x + 2500 = 24x – 20000
9x = 22500
x = 2500
CP = 3x – 2500 = 5000 - A shopkeeper marked a book 40% above the cost price and sold it after giving a discount of 30%, so that he made a loss of rs.4, what is the marked price of the article ?
240420280300320Option C
Let CP a book = 100x
MP = 100x * 140/100 = 140x
SP = 140x * 70/100 = 98x
loss = 100x – 98x = 2x
2x = 4
x = 2
MP = 140x = 140 * 2 = 280 - A dishonest salesman professes to sell his goods at the cost price but use faulty measure. His 1kg weight measures 950gms only. Find the gain percentage ?
200/6%15%20%100/19%28%Option D
Let CP = 950gm
SP = 1000gm
profit = 50
profit % = 50/950 * 100 = 100/19% - A person sells 18 chocolates, so that he losses the selling price of 2 chocolates. Find his loss percentage ?
5%10%8%12%20%Option B
Let SP of 1 chocolate = rs.1
SP of 18 chocolate = rs.18
loss = rs.2
CP = 18 + 2 = 20
loss % = 2/20 * 100 = 10% - A person bought two articles for rs.2000 and rs.2500 respectively. He sold first at a gain of 10%. At what price should he sell the other to get a profit of 20% on the whole transaction ?
32003000400045006500Option A
CP of first article = 2000
SP = 2000 * 110/100 = 2200
Total CP = 2000 + 2500 = 4500
total SP = 4500 * 120/100 = 5400
SP of second article = 5400 – 2200 = 3200 - A man sells the product for rs.800 and make some profit. If he sells it for rs.300 his loss is 2/3 of the earlier profit then what is the cost price of the product ?
400500650550740Option B
Let CP the product = x
SP = 800
profit = 800 – x
he sells for rs.300
loss = x – 300
(800 – x)2/3 = x – 300
1600 – 2x = 3x – 900
5x = 2500
x = 500 - A shopkeeper sells a table 4% discount on the marked price. The cost price of the table is 500 and he sells it at a profit of 20%, then what is marked price of the table ?
480320680625420Option D
CP of the table = 500
SP = 500 * 120/100 = 600
MP = 600 * 100/96 = 625 - Sita buys two books a total cost of rs.1400. She sells one for 3/4 of its cost and other for 2 times of its cost, so that she makes a profit of rs.400 on the whole transaction. What is the cost price of the lower price book.
600800500600700Option D
Total CP of the book = rs.1400
total SP of book = 1400 + 400 = 1800
Let CP of one book = x
CP of other book = 1400 – x
x * 3/4 + (1400 – x)^2 = 1800
x * 3/4 + 2800 – 2x = 1800
3x + 11200 – 8x = 7200
x = 800
CP of lower price book = 1400 – 800 = 600 - Sanju buys an old cycle for rs.1400 and spends rs.600 for its repair. After some days he sells his cycle at rs.2500, find profit percent of cycle ?
20%25%28%32%14%Option B
CP of cycle = 1400
he spend on it = 600
total CP = 1400 + 600 = 2000
he sold it = 2500
profit percentage = 500/2000 * 100 = 25% - The cost price of item Q is 300 more than the cost price item P. If item P was sold at a profit of 20% and item Q was sold at a loss of 40%. The ratio between selling price of P and Q is 8 : 7. What is the cost price of item Q ?
800700850640520Option B
Let cost price of item P = x
and item Q = x + 300
SP of item P = x * 120/100 = 6x/5
SP of item Q = (x + 300) 60/100 = (x + 300)3/5
(6x/5)/(x + 300)3/5 = 8/7
6x/5/3x + 900/5 = 8/7
42x = 24x + 7200
18x = 7200
x = 400
cost price of item Q = x + 300 = 700
89
Quantitative Aptitude: Simple/Compound Interest Set 22
- Sivam invested some money in a scheme at the rate of 20% for 3 years. If he withdraws 40% of total amount and left remaining amount is rs.2304. What is total money which he invested at earlier.
25002400350032004200Option B
Let principal = 100x
SI = 100x * 20/100 * 3 = 60x
Total amount = 100x + 60x = 160x
remaining = 160x * 60/100 = 96x
96x = 2304
x = 24
He invested = 100x = 2400 - Simple interest on rs.2750 for 2 years at certain rate of interest is rs.120 more than simple interest on rs.1500 for 3 years at same rate of interest. What is the rate of interest ?
12%14%15%13%18%Option A
Let rate of interest = R%
(2750*R/100*2) – (1500*R/100*3) = 120
55 R – 45R = 120
10 R = 120
R = 12% - Simple interest on a certain sum of money at rate of 20% for 2 years is two times of the compound interest on rs.5000 for 2 years at the rate of 14% per annum. What is the sum on simple interest ?
8340800012000749014000Option D
Rate of compound interest after 2 years = 14 + 14 + 14 * 14/100 = 29.96%
compound interest = 5000 * 29.96/100 = 1498
simple interest = 1498 * 2 = 2996
Let principal on simple interest = x
2996 = x * 20/100 * 2
x = 7490 - A man invested an amount of rs.4800 for 3 years a certain rate of simple interest become rs.7248. If the rate of interest increases by 3%, what amount will rs.5000 becomes in 2 years ?
72006320845082406830Option A
Simple interest = 7248 – 4800 = 2448
2448 = 4800 * 3 * 12/100
R = 17%
Now rate of interest = 17 + 3 = 20%
Amount = 5000 * 120/100 * 120/100 = 7200 - In how many years a sum will become four times itself at the rate of 12% per annum in simple interest ?
12 years24 years25 years26 years20 yearsOption C
Let the principal = x
Amount = 4x
Simple interest = 4x – x = 3x
3x = x * 12/100 * T
T = 25 years. - A deposited rs.6800 in a bank at 8% per annum for 5 years simple interest. B deposited rs.8000 at 20% per annum for 2 years in compound interest. What is difference between compound interest and simple interest.
850240836800840Option D
Simple interest = 6800 * 8/100 * 5 = 2720
By using successive,
20 + 20 + 20 * 20/100 = 44%
compound interest = 8000 * 44/100 = 3520
Difference = 3520 – 2720 = 800 - A certain sum in simple interest becomes rs.6600 in 4 years and becomes rs.7400 in 6 years, then find the rate of interest.
4%8%20%14%18%Option B
Simple interest for 2 years = 7400 – 6600 = 800
simple interest for 1 year = 400
simple interest for 4 years = 4 * 400 = 1600
sum = 6600 – 1600 = 5000
1600 = 5000 * R/100 * 4
R = 8% - The difference between compound and simple interests on a sum for 2 years at 15% per annum is 450. Find the sum.
1200025000200003800035000Option C
CI – SI = PR^2/100^2
450 = P * 225/10000
P = 20000 - The population of a town increased by 25% p.a. If the present population is 50000. Find the population of town 3 years ago.
2560024480325402400030340Option A
Let the population of town 3 year ago = x
x * 5/4 * 5/4 * 5/4 = 50000
x = 50000 * 64/125
x = 25600 - What is difference between compound interest and simple interest for 2 years on a principal of rs.4000 at the annual rate of 25% ?
340125250350300Option C
Simple interest = 4000 * 25/100 * 2 = 2000
Rate of compound interest after 2 years = 25 + 25 + 25 * 25/100 = 56.25%
compound interest = 4000 * 56.25/100 = 2250
difference = 2250 – 2000 = 250
90
Quantitative Aptitude: Number Series Set 150
- Directions : What will be come in place of questions ( ? ) marks in the following number series ?
20, 45, 100, 215, ?, 925320445245380450Option E
The series is (*2 + 5), (*2 + 10), (*2 + 15), (*2 + 20), (*2 + 25) - 48, 65, ?, 101, 120
8182807572Option C
The series is (7^2 – 1), (8^2 + 1), (9^2 – 1), (10^2 + 1 ), (11^2 – 1) - 8, 72, 172, 316, 512, ?
620768680540820Option B
The series is, (+8^2), (+10^2), (+12^2), (14^2), (+16^2) - 14, 42, 168, ?, 5040, 35280
840720680320580Option A
The series is (*3), (*4), (*5), (*6), (*7) - 26, 43, ?, 85, 114, 145
6075486254Option D
The series is (+17), (+19), (+23), (+29), (+31) - Directions : What will be wrong number in the following wrong number series ?
5, 10, 30, 150, 600, 36006001503600530Option B
The series is (*2), (*3), (*4), (*5), (*6) - 24, 16, 20, 32, 72, 184
20327218424Option B
The series is (*.5 + 4), (*1 + 4), (*1.5 + 4), (*2 + 4), (*2.5 + 4) - 14, 17, 27, 42, 68, 98
1442682798Option E
The series is +(2^2 – 1), +(3^2 + 1), +(4^2 – 1), +(5^2 + 1), (6^2 – 1) - 4, 10, 42, 254, 2034, 20362
442203420362254Option D
The series is, (*2 + 2), (*4 + 2), (*6 + 2), (*8 + 2), (*10 + 2) - 34, 48, 76, 118, 174, 248
342487648174Option B
The series is (+14), (+28), (+42), (+56), (+70)
91
Quantitative Aptitude: Simplification Questions Set 111
- Directions : What should be come in place of question ( ? ) marks in the following given below questions ?
32% of 480 + 25% of 680 – 20% of 380 = ?245240150247.6246.4Option D
153.6 + 170 – 76 = ?
? = 247.6 - 120% of 300 + (15)^2 – 290/2 = ?
230140440324520Option C
360 + 225 – 145 = ?
? = 440 - (18)^2 – 8 * (12)^2 + 320 * 15 = ?
34253972287532454972Option B
324 – 8 * 144 + 4800 = ?
? = 5124 – 1152
? = 3972 - 536 + 325 + 420 – 525 – 215 = ?
342240541640540Option C
1281 – 740 = ?
? = 541 - √4096 + √5776 – √4761 = ?
8232787146Option D
64 + 76 – 69 = ?
? = 71 - Directions : What should be come in place of question ( ? ) marks in the following given questions ? ( you are not calculate exact value )
24.99% of 599.98 + 178.01 = ? + 75.99302528120208252Option E
25% of 600 + 178 = ? + 76
150 + 178 = ? + 76
? = 328 – 76
? = 252 - 128.04 + (14.02)^2 – (8)^2 = ?
250260125234360Option B
128 + (14)^2 – 8^2 = ?
128 + 196 – 64 = ?
? = 324 – 64
? = 260 - 563.99 ÷ 12 + 242.01 + √1225 = ?
322228324422328Option A
564 ÷ 12 + 242 + 35 = ?
47 + 242 + 35 = ?
? = 322 - √1024.02 * 20.04 – 120 = ?
320480340520280Option D
√1024 * 20 – 120 = ?
? = 32 * 20 – 120
? = 640 – 120
? = 520 - 255.84 + (16.80 * 4) – (14)^2 = ?
128224250128256Option D
256 + (17 * 4) – (14)^2 = ?
? = 256 + 68 – 196
? = 324 – 196
? = 128
92
Partnership Questions Quantitative Aptitude: Partnership Set 21
- A ,B and C started a partnership business with investment in the ratio of 6 : 3 : 4. After one year A withdrawal half of his investment and B doubled his investment. Total profit of the business at the end of the two years is rs. 52000, then what is the sum of profit share of B and C ?
4200034000380005100040000Option B
Let the investment of A,B and C = 6x, 3x and 4x respectively.
profit sharing ratio of A,B and C = (6x * 1 + 3x * 1) : (3x * 1 + 6x * 1) : (4x * 2)
= 9x : 9x : 8x = 9 : 9 : 8
Total profit share of B and C = 52000 * 17/26 = 34000 - P started a business with the investment of rs.5500. After four months Q and R joined the business with investment of rs.6000 and rs.4500 respectively. At the end of the one year they earned total profit rs.22500. Find profit share of R ?
54007500500048503250Option A
profit sharing ratio of P,Q and R = (5500 * 12) : (6000 * 8) : (4500 * 8) = 11 : 8 : 6
profit share of R = 22500 * 6/25 = 5400 - Amit and Sumit invested rs.5000 and rs.7500 in a partnership business. After one year Amit added rs.2500 and sumit added rs.2000 in the business. If profit of Sumit at the end of two years is rs.13600, then find the total profit of the business ?
2080014500100002360028400Option D
Profit sharing ratio of Amit and Sumit = (5000 * 1 + 7500 * 1) : (7500 * 1 + 9500 * 1) = 25 : 34
profit share of sumit = 13600
total profit of the business = 13600 * 59/34 = 23600 - X,Y and Z started a business with investment ratio of 4 : 3 : 5. If they invested for 5 months, 8 months and 4 months respectively, then what is profit sharing ratio of X,Y and Z ?
4 : 2 : 52 : 5 : 310 : 9 : 53 : 4 : 85 : 6 : 5Option E
Profit sharing ratio of X, Y and Z = (4 * 5) : (3 * 8) : (5 * 4) = 20 : 24 : 20 = 5 : 6 : 5 - A and B investment rs.8000 and rs.6000 for 12 months and 14 months respectively in the business. If 25% of total profit is given to B as salary for managing business and remaining profit is distributed in their profit sharing ratio and profit share of A is rs.3200, then find total profit of the business ?
84006900480080004800Option D
Profit sharing ratio of A and B = (8000 * 12) : (6000 * 14) = 8 : 7
Let total profit of the business = 100x
salary given to B = 100x * 25/100 = 25x
remaining profit = 100x – 25x = 75x
profit share of A = 75x * 8/15 = 40x
40x = 3200
x = 80
total profit of the business = 100x = 100 * 80 = 8000 - Lipu and Papu start a business with initial investments in the ratio of 9 : 11 and their annual profit were in the ratio of 3 : 1. If Lipu invested the money for 11 months, then Papu invested his money for how many months ?
3 months8 months4 months14 months7 monthsOption A
Let Papu invested his money for x months.
9 * 11/ 11 * x = 3/1
x = 3 months - A , B and C enter into partnership business. A invests some money at the beginning, after 4 months B invests double the money of A’s invests and after 6 months C invests thrice the amount of A. If total profit of the business is rs.9200 at the end of one year, then how much profit B get ?
46002800340032003800Option D
Let A invests = rs.x
B invests = 2x
C invests = 3x
profit sharing ratio of A , B and C = (x * 12 ) : (2x * 8) : (3x * 6)
=6 : 8 : 9
profit share of B = 9200 * 8 /23 = 3200 - X , Y and Z entered into a partnership farm with investing rs. 12000, rs. 18000 and rs. 20000 respectively. X being a working partner gets 20% of the annual profit for the work. Find the profit share of X in an annual profit of rs. 25000 ?
86007300980058208750Option C
Profit sharing ratio of X , Y and Z = 12000 : 18000 : 20000 = 6 : 9 : 10
X gets profit for being a working partner = 25000 * 20 /100 = 5000
remaining profit = 25000 – 5000 = 20000
profit share of X of the remaining profit = 20000 * 6 /25 = 4800
total profit of X = 5000 + 4800 = 9800 - A and B started a business by investing rs.15000 and rs.20000 respectively. By mistake they divided the total profit in the ratio of 1 : 3, so that A loses rs.500. What is total profit of the business ?
14002400420028005200Option D
Profit sharing ratio of A and B = 15000 : 2000 = 3 : 4
Let total profit of the business = rs. x
profit sharing ratio of A = 3x/7
By mistake profit share of A = x/4
A losses = 500
= 12x – 7x/28
x = 500 * 28/5 = 2800
total profit of the business = rs.2800 - A and B started a business with capital of rs.28000 and rs.35000. After 6 months, A invests rs.4000 more, after 8 months B withdrawal rs. 5000 while C joins with capital of rs.40000. Annual profit of the business is rs.9200, then how much profit A get ?
43003600480052005500Option B
profit sharing ratio of A, B and C =(28000* 6 + 32000 * 6) : (35000 * 8 + 3000 * 4) : (40000 * 4) = 9 : 10 : 4
profit share of A = 9200 * 9/23 = 3600
93
Quantitative Aptitude: Quadratic Equations Questions Set 74
- I. x^2 – 13x – 198 = 0
II. y^2 – 21y + 108 = 0X > YX < YX ≤ YX ≥ YX= Y or no relation.Option E
I. x^2 – 22x + 9x – 198 = 0
x = 22, -9
II. y^2 – 12y – 9y + 108 = 0
y = 12, 9 - I. x^2 – 9x + 20 = 0
II. y^2 – 11y + 30 = 0X > YX < YX ≥ YX ≤ YX= Y or no relation.Option D
I. x^2 – 5x – 4x + 20 = 0
x = 5, 4
II. y^2 – 6y – 5y + 30 = 0
y = 6, 5 - I. x^2 – 30x + 216 = 0
II. y^2 – 34y + 168 = 0X > YX < YX ≥ YX= Y or no relation.X ≤ YOption D
I. x^2 – 18x – 12x + 216 = 0
x = 18, 12
II. y^2 – 28y – 6y + 168 = 0
y = 28, 6 - I. x^2 = 1024
II. y^2 – 38y + 192 = 0X > YX < YX ≥ YX ≤ YX= Y or no relation.Option E
I. x^2 = 1024
x = 32, -32
II. y^2 – 32y – 6y + 192 = 0
y = 32, 6 - I. x^2 – 27x + 92 = 0
II. y^2 + 22y + 112 = 0X > YX < YX ≤ YX ≥ YX= Y or no relation.Option A
I. x^2 – 23x – 4x + 92 = 0
x = 23, 4
II. y^2 + 14y + 8y + 112 = 0
y = -14, -8 - I. 4x^2 – 2x – 12 = 0
II. 3y^2 + 20y + 32 = 0X > YX < YX= Y or no relation.X ≤ YX ≥ YOption A
I. 4x^2 – 8x + 6x – 12 = 0
4x = 8, -6
x = 2, – 1.5
II. 3y^2 + 12y + 8y + 32 = 0
3y = -12, -8
y = -4, -2.67 - I. x^4 = 4096
II. y^2 – 28y – 160 = 0X > YX < YX ≤ YX= Y or no relation.X ≥ YOption C
I. x^4 = 4096
x = 8, -8
II. y^2 – 20y – 8y – 160 = 0
y = 20, 8 - I. x^2 – 20x + 96 = 0
II. y^2 + 3y – 28 = 0X > YX < YX ≤ YX ≥ YX= Y or no relation.Option A
I. x^2 – 12x – 8x + 96 = 0
x = 12, 8
II. y^2 + 7y – 4y – 28 = 0
y = -7, 4 - I. x^2 – x – 6 = 0
II. y^2 + 5x + 4 = 0X > YX < YX ≥ YX= Y or no relation.X ≤ YOption D
I. x^2 – 3x + 2x – 6 = 0
x = 3, -2
II. y^2 + 4y + y + 4 = 0
y = -4, -1 - I. x^2 – 5x – 84 = 0
II. y^2 – 32y + 252 = 0X > YX < YX ≥ YX= Y or no relation.X ≤ YOption B
I. x^2 – 12x + 7x – 84 = 0
x = 12, -7
II. y^2 – 14y – 18y + 252 = 0
y = 14, 18
94
Quantitative Aptitude: Ratio and Proportion Questions Set 10
- The ratio of monthly income of A , B and C is 5 : 8 : 3. If annual income of B is rs.192000, then what is the sum of the monthly income of A and C ?
1800040000140001600052000Option D
Let monthly income of A, B and C = 5x, 9x and 3x respectively.
Annual income of B = 12 * 8x = 96x
96x = 192000
x = 2000
sum of the monthly income of A and C = 5x + 3x = 8x = 8 * 2000 = 16000 - Three are two numbers in the ratio of 12 : 17. If 8 is substracted from each number the new numbers are in the ratio of 2 : 3. If 12 is added in each number then what will be the new ratio of the numbers ?
4 : 55 : 23 : 41 : 44 : 15Option C
Let two numbers are 12x and 17x respectively.
12x – 8/ 17x – 8 = 2/3
36x – 24 = 34x – 16
x = 4
two numbers are = (12 * 4), (17 * 4) = 48, 68
If we added 12 in each number, new ratio = (48 + 12) : (68 + 12) = 3 : 4 - There are two numbers in the ratio of 5 : 8. If 20 is added in first number and 6 is added in second number, then ratio of two numbers become 6 : 7. Find the larger of the two numbers ?
5048326428Option D
Let 1st numbers = 5x
2nd numbers = 8x
5x + 20/ 8x + 6 = 6/7
48x + 36 = 35x + 140
x = 8
Langer number = 8 * 8 = 64 - Total income of A, B and C is rs.57000. If A, B and C spend 60%, 80% and 82% of their income respectively and ratio of their saving is 8 : 5 : 9, then what is the income of B ?
1800020000250003300015000Option E
Let saving of A,B and C = 8x, 5x and 9x respectively.
income of A = 8x/40 * 100 = 25x
income of B = 5x/20 * 100 = 25x
Income of C = 9x/18 * 100 = 50x
Total income = 57000
income of B = 57000 * 25x/95x = 15000 - The ratio of salaries of P, Q and R is 5 : 4 : 6. If the salary of P, Q and R are increased by 20%, 25% and 32% respectively. Find the new ratio of their salaries.
5 : 8 : 33 : 8 : 93 : 5 : 630 : 25 : 4230 : 28 : 15Option D
Let salary of P, Q and R are 5x, 4x and 6x respectively.
new salary ratio = (5x * 120/100) : (4x * 125/100) : (6x * 140/100)
= 6x : 5x : 42x/5
= 30 : 25 : 42 - In what ratio should rice at rs.13 per kg and rs.20 per kg be mixed. So that the mixture be worth of rs.17 per kg ?
5 : 23 : 42 : 15 : 44 : 3Option B
By alligation method,
13 20
17
3 4
ratio = 3 : 4 - A bag has coins in the denominations of 50p, 25p and 20p in the ratio of 4 : 2 : 1. If the total value of the coins is rs.108. Find the number of 20p coins in the bag ?
50804540240Option D
Let the number of 50p, 25p, and 20p coins in the bag are 4x, 2x and x respectively.
(50 * 4x) + (25 * 2x) + (20 * x) = 10800p
200x + 50x + 20x = 10800
270x = 10800
x = 40
number of 20p coins = 40 - First number and second number are 32% and 48% more than the third number. Find the ratio of first number, third number and second number.
33 : 25: 3733 : 37 : 2533 : 38 : 255 : 7 : 86 : 5 : 3Option A
Let third number = 100
first number = 100 * 132/100 = 132
second number = 100 * 148/100 = 148
ratio of first, third and second number = 132 : 100 : 148 = 33 : 25 : 37 - A marriage party is attended by a total of 80 persons. If the ratio of men and women in the party is 3 : 2, how many more women must join the party such that the ratio becomes 6 : 5 ?
41214819Option D
Total persons = 80
men = 80 * 3/5 = 48
women = 80 * 2/5 = 32
Let the number of women will join = x
48/32 + x = 6/5
192 + 6x = 240
x = 8 - The students of three class are in the ratio of 5 : 6 : 4. If 8 students of each class increased so that, the ratio becomes 6 : 7 : 5, then Find the total number of students in the class before increased ?
140120165200170Option B
Let the number of students in 1st, 2nd and 3rd class are 5x, 6x and 4x respectively.
5x + 8/6x + 8 = 6/7
36x + 48 = 35x + 56
x = 8
total students of class before increased= 5x + 6x + 4x = 15x = 15 * 8 = 120
95
Quantitative Aptitude: Data Sufficiency Questions Set 15
- what is distance between city A and city B ?
I. Sanju and Manju started their journey simultaneously from city A to city B with their speeds in the ratio of 3 : 2.
II. Manju takes 2 hours more than Sanju to reach city B.
II. The difference between speeds of Sanju and Manju is 25 km/hr.Only I and II is sufficient.Only II and III is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.All I, II and III are sufficient.Option E
From I, Let speed of Sanju = 3x
speed of Manju = 2x
From II, we can not calculate distance between city A and B.
From III, difference between speed of Sanju and Manju is given, so we can not calculate the answers.
from statement, I, II, III together,
Difference between their speeds = 3x – 2x = 25
x = 25
speed of Sanju = 3 * 25 = 75
speed of Manju = 2 * 25 = 50
Let distance = D
D/50 – D/75 = 2
3D – 2D/150 = 2
D = 300 - In how many days will B alone completed the work ?
I. A and B together can complete the work in 16 days.
II. B and C together can complete the work in 12 days.
III. A and C together can complete the work in 18 days.Only I and II is sufficient.Only II and III is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.All I , II and III are sufficient.Option E
From I, only from statement I we can not get the answer.
From I and II,
LCM of 16 and 12 = 144
Total work = 144
efficiency of A and B = 144/16 = 9
efficiency of B and C = 144/12 = 12
Here, we can not get answers.
From I, II and III,
efficiency of A and C = 144/18 = 8
A + B + B + C + A + C = 9 + 12 + 8 = 29
A + B + C = 29/2 = 14.5
Here, we can get the answers. - What will be the difference between two numbers ?
I. the square of the first numbers is 9 times the second number.
II. The ratio of the first number to the second number is 3 : 4.Only I is sufficient.Only II is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option E
From I, we can not calculate the answers.
From I and II, Let first numbers = 3x
second number = 4x
(3x)^2 = 9 * 4x
9x^2 = 36x
x = 4
Difference = (4 * 4) – (3 * 4) = 4 - What was the percent profit or loss incurred by selling an article for rs.14000 ?
I. The ratio of selling price to the cost price of the article is 7 : 5.
II. The marked price of the article is 60% more than the cost price.Only I is sufficient.Only II is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option A
From I,
Ratio of SP and CP of the article = 7 : 5
SP = 14000
CP = 14000/7 * 5 = 10000
profit % = (14000 – 10000)/10000 * 100 = 40%
only statement I is sufficient. - What is the amount invested in scheme B ?
I. The amount invested in scheme A is rs.48000.
II. The amount invested in scheme A is 60% of the total amount invested.
III. The amount invested in scheme A and B are in the ratio of 3 : 2.Only I and II is sufficient.Only I and III is sufficient.Either only I and II or only I and III is sufficient.Neither I nor II is sufficient.All I, II and III are sufficient.Option C
From I, invested by A = 48000
from I and II,
Let, total investment of A and B = 100x
investment of A = 60x
investment of B = 40x
ratio of investment A and B = 3 : 2
investment of B = 48000/3 * 2 = 32000
From I and III,
Investment of A = 48000
Investment ratio of A and B = 3 : 2
investment of B = 48000/3 * 2 = 32000
either only statement I and II or only statement I and III is sufficient. - What is the present age of B ?
I. The age of B is 4 years older than A.
II. The ratio of present age of A and C is 5 : 4.Only I is sufficient.Only II is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option D
From I,
We can not get answer,
from I and II,
Let present age of A and C = 5x and 4x respectively.
the age of B = 5x + 4
from I and II together we can not get answer. - What is the speed of boat in still water ?
I. The boat can go a distance of 320 km in 8 hours in downstream speed.
II. The ratio of downstream speed and upstream speed is 5 : 3.Only I is sufficient.Only II is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option E
From I,
Downstream speed = 320/8 = 40 km/hr
only statement I is not sufficient.
From I and II,
Downstream speed = 40 km/hr
upstream speed = 40/5 * 3 = 24 km/hr
speed of boat in still water = (40 + 24)/2 = 32 km/hr
both statement I and II is required to get answer. - Find the rate of interest ?
I. The difference between CI and SI on an amount at rs.4000 for 2 years is rs.90.
II. The simple interest incurred on certain sum is rs.2400 in 4 years.Only I is sufficient.Only II is sufficient.Either I or II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option A
From I,
CI – SI = PR^2/100^2
90 = 4000 * R^2/10000
R = 15%
From II, Here principal is not given so we can not get answer.
only statement I is sufficient. - What is the length of rectangle ?
I. The perimeter of square field is 56m and breadth of the rectangle filed is 4m more than the side of square field.
II. The area of rectangular field is 360 m^2.Only I is sufficient.Either I or II is sufficient.Only II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option E
From I,
Perimeter of square filed = 56m
side of square = 56/4 = 14m
breadth of rectangular field = 14 + 4 = 18 m
Here we can not get answer.
From I, and II,
Breadth of rectangular = 14 + 4 = 18
Area of rectangular = 360 m^2
length = 360/18 = 20m
both I and II is required to get answer. - What is the length of train B ?
I. Length of train A is 180 m and it crosses a pole in 12 seconds.
II. The ratio of speed of train A and train B is 3 : 5. Train B crosses a 280 m long bridge in 20 seconds.Only I is sufficient.Either I or II is sufficient.Only II is sufficient.Neither I nor II is sufficient.Both I and II are sufficient.Option E
From I, length of train A = 180 m
speed of train A = 180/12 = 15 m/sec
only statement I is not sufficient.
Both from I and II,
speed of train B = 15/3 * 5 = 25 m/sec
let length of train B = x
x + 280/20 = 25
x = 220
both statement I and II is required to get answer.
96
Quantitative Aptitude: Simple/Compound Interest Set 21
- The difference between compound interest and simple interest on rs.42000 at same rate of interest for 2 years is rs.945. What is the rate of interest ?
10%15%14%20%25%Option B
945 = PR^2/100^2
945 = 42000 * R^2/10000
R^2 = 225
R = 15% - Rohit borrows rs.4000 at 10% on compound interest and at the end of the every year he paid rs.1000 back. How much amount should he pay at the end of the 3rd year to settlement all his debt ?
25003000324030142480Option D
total amount at the end of the 1st year = 4000 * 110/100 = 4400
After he paid rs.1000, remaining amount = 4400 – 1000 = 3400
total amount at the end of 2nd year = 3400 * 110/100 = 3740
After he paid rs.1000, remaining amount = 3740 – 1000 = 2740
total amount at the end of 3rd year = 2740 * 110/100 = 3014
At the end of 3rd year he paid 3014 to settlement his debt. - A man borrows rs.8000 for 3 years and he gave at 15%, 20% and 30% rate of interest for 1st year, 2nd year and 3rd year respectively. Then how much amount he paid at the end of 3rd years in compound interest ?
1443514352172501954020450Option B
Amount in 1st year = 8000 + (8000*15/100) = 9200
Amount in 2nd year = 9200 + (9200*20/100) = 11040
Amount in 3rd year = 11040 + (11040 * 30/100) = 14352 - What is the compound interest on rs.8600 at 20% p.a. for 1 years, compounded half yearly.
22402420144018061425Option D
Rate of interest for 1 year = 20%
rate of interest for half year = 10%
by applying successive,
10 + 10 + 10 * 10/100 = 21%
compound interest = 8600 * 21/100 = 1806 - Shivam invested a certain amount at the rate of 14% for 4 years in simple interest and after 4 years he obtained a total simple interest of rs.5600. If invested the same amount at the same rate of interest for 2 years in compound interest then how much interest would he have obtained ?
32202996283424502830Option B
Let principal be rs. x
= x * 14/100 * 4 = 5600
x = 5600 * 100/56 = 10000
by applying successive, rate of compound interest = 14 + 14 + 14 * 14/100 = 19.96%
compound interest = 10000 * 29.96/100 = 2996 - The difference between simple interest and compound interest on a certain sum at 20% rate of interest for 2 years is 500. What is difference between simple interest and compound interest for 1st year, if interest is compounded half-yearly ?
120180125150190Option C
500 = PR^2/100^2
500 = P * 400/10000
P = 12500
simple interest for 1st year = 12500 * 20/100 = 2500
Rate of interest for compound half yearly = 20/2 = 10%
by apply successive method,
rate of CI = 10 + 10 + 10 * 10/100 = 21%
compound interest = 12500 * 21/100 = 2625
Difference = 2625 – 2500 = 125 - On a certain sum of money simple interest occurred after 4 years is rs.4800 and compound interest occurred after 2 years is rs.2580. If rate of interest in both cases are same, find the principal amount ?
120008000140001800020000Option B
SI after 4 years = 4800
SI for 1 year = 4800/4 = 1200
SI for 2 years = 2400
CI for 2 years = 2580
by applying SI and CI ratio formula,
SI/CI = 200/200 + r
2400/2580 = 200/200 + r
r = 15%
Let principal = rs. x
x * 15/100 * 4 = 4800
x = 4800*100/60 = 8000 - What is difference between compound interest and simple interest for 2 years at the rate of 20% on a principal of rs.8500 ?
240520340624125Option C
SI for 2 years = 8500 * 20/100 * 2 = 3400
by applying successive
rate of compound interest after 2 years = 20 + 20 + 20 * 20/100 = 44%
CI = 8500 * 44/100 = 3740
Difference = 3740 – 3400 = 340 - If a money get tripled in 5 years on a certain rate of simple interest, then find the rate of interest ?
20%40%48%45%25%Option B
let principal = rs. x
amount = 3 * x = 3x
simple interest = 3x – x = 2x
2x = x * R/100 * 5
R = 40% - Shiva invested rs. X for 4.5 years at the rate of 20% p.a. on simple interest. If he received rs.2520 as interest, then what is the value of X ?
28001700340046003800Option A
2520 = X * 20/100 * 4.5
X = 2800
97
Quantitative Aptitude: Probability Questions – Set 20
- A bag contains 8 green balls and 12 blue balls. If a ball is drawn randomly, then find the probability of getting either green ball or blue ball.
232/52/31Option E
required = (8C1) + (12C1) = 20
total = (20C1) = 20
probability = 20/20 = 1 - If two cards are drawn randomly from a pack of 52 cards. Then what is the probability of both cards are red cards ?
28/9123/10825/102817Option C
required = (26C2) = 13 * 25
Total = (52C2) = 26 * 51
probability = (13 * 25)/(26 * 51) = 25/102 - How ,any 4-digit numbers can be formed from the digits 6, 2, 5, 7, 3, which are divisible by 5 and none of the digits is repeated ?
140220282496Option D
A number to be divisible by 5, unit digit must be 0 or 5.
So, in 4-digit numbers unit place is required to be filled by digit 5 and rest three places of required 4-digit numbers will be filled by rest 4 digit.
numbers of ways = 4! = 4 * 3 * 2 * 1 = 24 - Out of 52 playing cards two cards is picked randomly, then what is the probability of getting that one red king and one black queen ?
2/6635/138/58514Option A
required = (2C1) * (2C1) = 4
Total = (52C2) = 26 * 51
probability = 4/(26*51) = 2/663 - A bag contains 2 red pens, 6 blue pens and 4 green pens. Find the probability of getting two same color pens from the bag ?
5/82/41/35/64Option C
required = (2C2) + (6C2) + (4C2)
= 1 + 15 + 6 = 22
total = (12C2) = 66
probability = 22/66 = 1/3 - A basket contains 3 green, 4 orange and 5 pink balls. If two balls are drawn randomly from the basket, then what the probability of selecting that both balls are of different colors ?
4/6557/688/4547/664/15Option D
possibility of both balls are different colors = ( 1 green and 1 orange) , (1 orange and 1 pink ), (1 green and 1 pink)
required = (3C1) * (4C1) + (4C1) * (5C1) + (3C1) * (5C1)
= 12 + 20 + 15 = 47
total = (12C2) = 66
probability = 47/66 - Sunil threw two dices together. What is the probability of getting that the sum of the two outcomes is 4 ?
1/81/12452Option B
Possibility to get = (2, 2), (3, 1), (1, 3)
required = 3
total = 36
probability = 3/36 = 1/12 - When three coins are tossed simultaneously, then find the probability of getting at least one tale.
7/85/81/44/152Option A
possibility = 1 tale or 2 tale or 3 tale
required = (3C1) + (3C2) + (3C3)
= 3 + 3 + 1 = 7
total = 2^3 = 8
probability = 7/8 - Four boys and 2 girl sit in a row for presenting their project paper, then what is the probability that they will sit in alternate position ?
1/62/31/81/152/5Option D
probability = 4! * 2!/6! = 1/15 - Probability of a question solved by A and B is 1/5 and 1/4 respectively, then find the probability that at least one of them will solve the questions ?
5/61/411/252/55/9Option D
possibility = 1 – probability of question not solved by anyone
probability = 1 – (1 – 1/5) * (1 – 1/4)
= 1-(4/5) * (3/4)
= 2/5
98
Quantitative Aptitude: Mensuration Questions Set 15
- The ratio of length and breadth of rectangular field is 3 : 2. If the perimeter of rectangular field is 40cm, then what is the area of square whose side 5cm more than the length of rectangular field ?
216289324196400Option B
Let length and breadth or rectangular field = 3x and 2x
perimeter = 40
2(3x + 2x) = 40
10x = 40
x = 4
length = 3 * 4 = 12cm
side of square = 12 + 5 = 17
Area of square = 17 * 17 = 289 cm^2 - Length of two rectangles A and B is 14 cm and 20 cm respectively and sum of their breadth 14 cm. If ratio of perimeter of A and B is 5 : 7, then what is the difference between area of these rectangles ?
8454426276Option E
Let breadth of rectangular A = x
and breadth rectangular B = 14 – x
perimeter of rectangular A = 2 (14 + x)
perimeter of rectangle B = 2 (20 + 14 – x)
= 2 (34 – x)
2 (14 + x)/2 (34 – x) = 5/7
340 – 10x = 196 + 14x
x = 6
breadth of rectangle A = 6 cm
breadth of rectangle B = 14 – 6 = 8 cm
Area of rectangle A = 14 * 6 = 84 cm^2
Area of rectangle B = 20 * 8 = 160 cm^2
Difference = 160 – 84 = 76 cm^2 - If the diagonal of a cube is of length ‘x’, then what is the lateral surface area of that cube ?
2x^2/35x/34x/34x^2/38xOption D
Diagonal of cube = a√3
a√3 = x
a = x/√3
lateral surface area = 4a^2 = 4*(x/√3)^2 = 4x^2/3 - If the total surface area of a cube is 8664 cm^2, the what is the length of its diagonal ?
46√334√338√324√319√2Option C
T.S.A = 8664
6a^2 = 8664
a^2 = 1444
a = 38
diagonal = a√3 = 38√3 - If the ratio of radius of two spheres A and B is 3 : 5, then what is the ratio of their volumes ?
27 : 1253 : 512 : 259 : 256 : 15Option A
Ratio of volume of A and B = 4/3π(3)^3 : 4/3π(5)^3
= 27 : 125 - The ratio of length and breadth of rectangles is 5 : 3 and its area is 240 m^2. If the perimeter of square is 8m less than the perimeter of rectangles, then what is the area of square ?
324196102414441296Option B
Let length and breadth of rectangles = 5x and 3x
Area = 240
15x^2 = 240
x = 4
length = 5 * 4 = 20
breadth = 3 * 4 = 12
perimeter of rectangle = 2 (20+ 12) = 64
perimeter of square = 64 – 8 = 56
side of square = 56/4 = 14
Area of square = 14 * 14 = 196 - The non – parallel sides of a trapezium are equal to side of perimeter of square 40cm and the parallel sides are 8cm and 20cm respectively, find the perimeter of trapezium ?
3824203640Option D
perimeter of square = 40
side of square = 40/4 = 10cm
non-parallel side of trapezium = 10
one parallel side = 8cm
other parallel side = 20cm
breadth of tringle = 20 – 8/2 = 6
let height of trapezium = h
10^2 = h^2 + 6^2
h^2 = 64
h = 8
perimeter = 10 + 10 + 8 + 8 = 36 cm - The circumference of a circle A is equal to the perimeter of a square whose area is 1936 m^2. Diameter of circle B is four times the radius of circle A what is the area of circle B ?
45323952284049009856Option E
Area of square = 1936 m^2
side of square = √1936 = 44m
perimeter of square = 44 * 4 = 176m
2πr = 176
r = 176 *7 /44 = 28
diameter of circle B = 28 * 4 = 112
radius = 112/2 = 56m
Area = πr^2 = 22/7 * 56 * 56 = 9856 - If the height and radius of a cylinder increased by 25% and 20% respectively. Then what is the change in percent in its curved surface area ?
20%50%40%25%58%Option B
Let the height of cylinder = 4h
increased height = 4h* 125/100 = 5h
and radius of cylinder = 5r
increased radius = 5r * 120/100 = 6r
initial curved surface area = 2 * π * 4h * 5r = 40πhr
new curved surface area = 2 * π * 5h * 6r = 60πhr
% change = 60πhr – 40πhr/40πhr * 100 = 50% - The length , breadth and height of a cuboid is 14m, 15m, 20m respectively,. Find the lateral surface area of cuboid ?
12251160425024203840Option B
L.S.A = 2 * 20 (14 + 15) = 40 * 29 = 1160 m
99
Mixed Quantitative Aptitude Questions Set 217
- Train A crosses a 400m long bridge and a pole in 32 second and 12 seconds respectively. If length of train B is 40m more then the length of train A and speed of train B is 32m/sec. Then how much time required if train A and B is running in opposite direction ?
14 sec4 sec18 sec10 sec19 secOption D
Let length of train A = x
x+400/32 = x/12
32x = 12x + 4800
20x = 4800
x = 240
speed of train A = 240/12 = 20m/sec
length of train B = 240 + 40 = 280m
speed of train B = 32m/sec
Time = 240 + 280/32 + 20 = 520/52 = 10sec - The ratio of number of male and female in a group is 8 : 5. If the percentage of male and female increased by 20% and 25% respectively. Then find the new ratio of male and female, if total number of male and female is 260 initially.
8 : 35 : 47 : 85 : 34 : 11Option D
Total number of male and female = 260
number of male = 260 * 8/13 = 160
number of female = 260 * 5/13 = 100
increased male = 160 * 5/4= 200
increased female = 100 * 6/5 = 120
ratio = 200 : 120 = 5 : 3 - The ratio of age of A and B before 5 years is 2 : 3 and D is 12 years elder than B. The present age of C is one fourth of the present age of D. If the age of C after 6 years is 14 years, then find the present age of B.
28 years20 years34 years38 years42 yearsOption B
Let the age of A and B before 5 years = 2x and 3x
present age of A = 2x + 5
present age of B = 3x + 5
present age of D = 3x + 5 + 12 = 3x + 17
present age of C = 3x + 17/4
present age of C = 14 – 6 = 8 years
3x + 17/4 = 8
3x + 17 = 32
3x = 32 – 17
3x = 15
x = 5
present age of B = 3x + 5 = 20 years. - A bag contain 4 red pens, 6 green pens and 8 blue pens. If 2 pens are taken at randomly, then find the probability that there are no blue pens.
8/175/178/152/84Option B
required = 10C2 = 10 * 9/2 * 1 = 45
total = 18C2 = 18 * 17 / 2*1 = 153
probability = 45/153 = 5/17 - Shiva invested rs.4200 in a scheme at 18% per annum for 3 years at simple interest and he also invested same amount in another scheme at 20% per annum for 3 years. What is the difference between simple interest and compound interest which he earned from both the scheme ?
880789.6435.6940840Option B
simple interest = 4200*18/100*3 = 2268
by applying successive method,
20 + 20 + 400/100 = 44%
44 + 20 + 880/100 = 72.8
compound interest = 4200 * 72.8/100 = 3057.6
Difference = 3057.6 – 2268 = 789.6 - Directions : what will be the wrong number in the following wrong number series ?
34, 35, 43, 52, 116, 945116435294534Option D
The series is (+1)^2, (+2)^3, (+3)^2, (+4)^3, (+5)^2 - 18, 10, 11, 17.5, 36, 94
17.510183694Option E
The series is (*.5 + 1), (*1 + 1), (*1.5 +1), (*2 + 1) , (*2.5 + 1) - 52, 56, 65, 90, 139, 260
52566590260Option B
The series is, (+2)^2, (+3)^2, (+5)^2, (+7)^2, (+11)^2 - 5, 8, 21, 70, 290, 1461
52908146170Option B
The series is (*1 + 3), (*2 + 5), (*3 + 7), (*4 + 9), (*5 + 11) - 153, 161, 177, 215, 233, 273
161177233215233Option D
The series is, (+8), (+16), (+24), (+32), (+40)
100













